膜生物反应器“两次分离”数学模型分析及建立
膜生物反应器是由超(微)滤膜组件和生物反应器构成的。传统超(微)滤过程的进料一般为单相流体(即只有液相),而膜生物反应器中超(微)滤分离的活性污泥混合液却是固—液两相流体,既包括活性污泥悬浮固体,也包括液体以及溶解在其中的有机物质,膜不但要截留大分子有机物,而且要分离固体颗粒。因此,固体颗粒在错流中的迁移规律(包括固体颗粒在剪切流中的运动规律以及固体颗粒在膜面的沉积规律)就必然会对整个膜分离过程产生影响,对此过程进行分析并建立新的数学模型加以描述是十分有意义的。
1 固体颗粒在错流过滤中的迁移规律
在错流过滤中,固体颗粒的运动受沿膜面平行流动的剪切流和垂直于膜面的过滤渗透流的共同作用。渗透流趋向于将固体颗粒曳向膜面,而剪切流力图保持颗粒悬浮,将其随循环液带出膜面。固体颗粒是沉积于膜面还是随循环液流出,取决于剪切流和渗透流曳力的相互作用结果。
固体颗粒迁移运动趋于膜面的速率和流出膜组件的横向迁移速率应该和颗粒直径、流道几何尺寸、剪切流速率和膜渗透过滤速率有关。
借用Alter和Belfort固体颗粒在错流微滤过程中的迁移机理,对于达到稳定状态时,即膜面的渗透过滤速率保持稳定时,颗粒迁移运动趋于膜面的速率为:
VP=Vm[g(β)+Rewh2(β)] (1)
式中 VP——颗粒迁移运动趋于膜面的速率
Vm——膜渗透过滤速率
Rew——渗透系数
β——流道无量纲宽度
g(β)、h2(β)——β的函数
颗粒横向迁移速率为:
Ve=Rep(dp/2B)2umf(β ) (2)
式中 Ve ——颗粒横向迁移速率
um——流道剪切流速率
dp——颗粒直径
B——流道宽度
Rep——系数
f(β)——β的函数
由式(1)、(2)可见,颗粒迁移运动趋于膜面的速率与膜渗透过滤速率成正比;颗粒横向迁移 速率与流道剪切流速率成正比。
2 固体颗粒沉积阻力模型的建立
错流过滤中,固体颗粒在过滤渗透流和剪切流的综合作用下,有向膜面沉积的趋势。随着过滤的进行,会在膜面逐步形成沉积层。沉积层累积阻力Rd可由下式确定:
Rd=αd·Md (3)
式中 Rd ——固体颗料沉积层累积阻力
αd——比阻
Md——沉积负荷(单位膜面积的沉积量)
比阻αd可由Kozeny—Carman关系计算:
αd=180(1-ε)2/(ds2ε3) ( 4)
式中 ε ——沉积层孔隙率
ds——固体颗粒粒径
由式(4)可见,沉积层愈密实,固体颗粒粒径愈小,沉积层比阻愈大。
比阻受操作压力P的影响,并有:
αd=αd0·Pn (5)
式中 αd0——系数
n——压缩系数
由超滤过程的阻力模型得膜通量为:
Jv=P/μ(Rm+Rd)=P/μ·R 总 (6)
式中 Rm ——膜本身的阻力
Rd——累积阻力
R总——总阻力
P——膜组件的操作压力
μ——动力粘滞系数
将式(3)、(5)代入式(6)中,有:
Jv=1/μ(P/(Rm+αd0M dPn)) (7)
当操作压力较大时,Rm<αd0MdPn,膜通量可近等于:
Jv=1/μ(P1-n/αd0 Md ) (8)
由于在操作压力较大时已形成凝胶层,在此情况下,Jv已基本与P无关,亦即相当于n=1,故式(7)可简化为:
Jv=1/μ[P/(Rm+αd0MdP)] (9)
3 “两次分离”模型的建立
在膜生物反应器中,膜分离不仅要实现活性污泥混合液的固液分离,而且还要实现大分子有 机物与水的分离。因此提出膜生物反应器的“两次分离”观点:
①膜对活性污泥混合液的分离过程是由两次分离实现的,一次分离是混合液在压力作用下进行固液分离,即混合液中的液相与活性污泥的固体颗粒分离,其相当于一个压缩脱水过程,水中的溶解性有机物及部分胶体物质随液相分离出来,而固体颗粒则在其迁移运动中逐步形成沉积层。二次分离是分离出来的液相透过沉积层到达膜表面,实现有机物大分子及胶体物质与水的分离。大分子有机物被截留在膜面形成浓差极化并逐步发展为凝胶层,水透过膜形成透过液。
②固液分离过程可用阻力模型来描述;而膜表面有机物大分子与水的分离可用凝胶极化模 型描述。
③稳态时,固液分离的速率与有机物大分子和水分离的速率相等。
上述假定用图1表示。
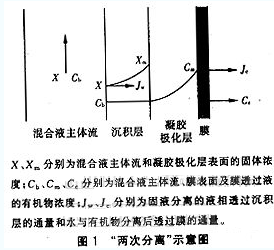
根据上述假定,固液分离过程可表述为:
Jw=1/μ[P/(Rm+αd0MdP)] (10)
要描述膜表面有机物大分子与水的分离,根据超滤分离的凝胶极化模型有:
Jc=kln(Cm-Ce)/(Cb-Ce) (11)
式中 k——物质迁移系数
令Jw=Jc,有:
1/μ[P/(Rm+αd0MdP )]=kln[(Cm-Ce)/(Cb-Ce)] (12)
引入膜对溶质的表观分离率R=1-(Ce/Cb) ,代入式(12)并整理得:
Cm/Cb=R{exp[(1/μ·k)( P/Rm+αd0MdP)]-1}+1 (13)
若Ce足够小,则有:
Cm=Cbexp[(1/μ·k)(P/(Rm+ αd0MdP)] (14)
式(13)、(14)综合地反映了膜生物反应器中,膜分离活性污泥混合液时固体颗粒的沉积和大分子有机物的浓差极化之间的相互作用,体现了操作条件(膜面流速u含在k中)与有机物浓度之间的相互关系,可以作为描述膜生物反应器“两次分离”观点的数学模型。
膜生物反应器“两次分离”观点的提出及其数学模型的建立,主要是依据理论分析,如何进一步验证该观点及其数学模型并使其具有可操作性,尚需在分子水平上对膜生物反应器的分离机理进行深入研究。
