§7.6将地面观测的方向值归算到椭球面
我们知道,参考椭球面是测量计算的基准面,而野外的各种测量工作都是在地面上进行的,测站点和照准点一般都超过参考椭球面一定高度,观测的基准线不是各点相应的椭球面的法线,而是各点的垂线,各点的垂线与法线间存在着垂线偏差,因此,也就不能直接在地面上处理观测成果,而应将地面观测的元素(方向和距离等)归算至椭球面上。在归算中有两条基本要求:(1)以椭球面的法线为基准;(2)将地面观测元素化为椭球面上大地线的相应元素。本节主要研究方向值的归算。
7.6.1将地面观测的水平方向归算至椭球面----三差改正
将水平方向归算至椭球面,包括垂线偏差改正、标高差改正及截面差改正,习惯上称此三项为三差改正。
1.垂线偏差改正![]()
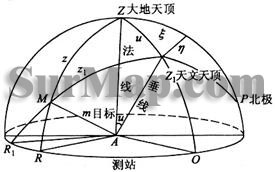 地面上所有水平方向的观测都是以垂线为根据的,而在椭球面上则要求以该点的法线为依据。因此在每三角点上,把以垂线为依据的地面观测的水平方向值归算到以法线为依据的方向值而应加的改正定义为垂线偏差改正。
地面上所有水平方向的观测都是以垂线为根据的,而在椭球面上则要求以该点的法线为依据。因此在每三角点上,把以垂线为依据的地面观测的水平方向值归算到以法线为依据的方向值而应加的改正定义为垂线偏差改正。
垂线偏差改正同经纬仪垂直轴改正相似,以测站A为中心作出单位半径的辅助球,u是垂线偏差,它在子午圈和卯酉圈上的分量分别为![]() 为准,照准m点得
为准,照准m点得![]() 。
。
垂线偏差的计算公式为:
![]()
![]() (7-86)
(7-86)
式中![]() 是测站点上的垂线偏差在子午圈和卯酉圈上的分量,它们可在测区的垂线偏差分量图中内差取得,从(7-86)式中可以看出,垂线偏差改正的数值主要与测站点的垂线偏差和观测方向的天顶距(或垂直角)有关。
是测站点上的垂线偏差在子午圈和卯酉圈上的分量,它们可在测区的垂线偏差分量图中内差取得,从(7-86)式中可以看出,垂线偏差改正的数值主要与测站点的垂线偏差和观测方向的天顶距(或垂直角)有关。
2.标高差改正![]()
![]() 不在同一平面内,故在A点照准B点得出的法截线是Ab/而不是Ab,因而产生了Ab同Ab/方向的差异。按归算的要求,地面各点都应沿自己法线方向投影到椭球面上,即需要的是Ab方向值而不是Ab/方向值,因此需加入标高差改正数
不在同一平面内,故在A点照准B点得出的法截线是Ab/而不是Ab,因而产生了Ab同Ab/方向的差异。按归算的要求,地面各点都应沿自己法线方向投影到椭球面上,即需要的是Ab方向值而不是Ab/方向值,因此需加入标高差改正数![]() ,以便将Ab/方向改到Ab方向。
,以便将Ab/方向改到Ab方向。
标高差改正的计算公式为:
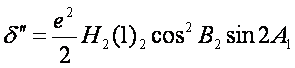 (7-87)
(7-87)
式中![]() 为照准点高出椭球面的高程,它由三部分组成:
为照准点高出椭球面的高程,它由三部分组成:
![]() (7-88)
(7-88)
![]() 为照准点的觇标高
为照准点的觇标高
其中![]() 相应的子午圈曲率半径。实用中为计算方便,设
相应的子午圈曲率半径。实用中为计算方便,设
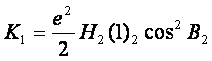 (7-89)
(7-89)
则(7-87)式变为: ![]() (7-90)
(7-90)
![]() 为引数查取。
为引数查取。
由上可知,标高差改正主要与照准点的高程有关。经此项改正后,便将地面观测的水平方向值归化为椭球面上相应的法截弧方向。
![]()
在椭球面上,纬度不同的两点由于其法线不共面,所以在对向观测时相对法截弧不重合,应当用两点间的大地线代替相对法截弧。这样将法截弧方向化为大地线方向应加的改正叫截面差改正,用![]() 表示。
表示。
AaB是A至B的法截弧,它在A点处的大地方位角为![]() 就是截面差改正。截面差改正计算公式为
就是截面差改正。截面差改正计算公式为
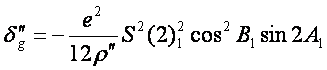 (7-91)
(7-91)
式中S为AB间大地线长度,![]() 相对应的
相对应的
卯酉圈曲率半径。
令 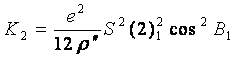 (7-92)
(7-92)
则(7-81)式变为: ![]() (7-93)
(7-93)
![]() 为引数查取。由上式可知,截面差改正主要与测站点至照准点间的距离S有关。
为引数查取。由上式可知,截面差改正主要与测站点至照准点间的距离S有关。
4.三差改正的计算
为了在内业计算时不影响外业观测精度,各等三角测量在归算时对取位的要求是不同的。按作业中的有关规定:一等需算至0.001//;二等为0.01//;三等和四等为0.1//。那么是不是各等三角测量都需加入三差改正呢?我们先看一下三差改正的数量级:![]()
(1)设A=![]() 时
时
|
H |
|
|
200m |
0.01// |
|
1000m |
0.05// |
|
2000m |
0.1// |
|
|
|
|
5// |
0.05// |
|
10// |
0.1// |
(3)设![]()
|
S |
|
|
30km |
0.001// |
|
60km |
0.005// |
由此可以看出,在一般情况下,一等三角测量应加三差改正;二等三角测量应加垂线偏差改正和标高改正,而不加截面差改正;三等和四等三角测量可不加三差改正,但当![]() 或H>2000m时,则应分别考虑加垂线偏差改正和标高差改正。即对特殊情况应依测区实际情况具体分析,然后再确定是否加入三差改正。经过三差改正后,最后得到椭球面上相应的各大地线的方向值。
或H>2000m时,则应分别考虑加垂线偏差改正和标高差改正。即对特殊情况应依测区实际情况具体分析,然后再确定是否加入三差改正。经过三差改正后,最后得到椭球面上相应的各大地线的方向值。
7.6.2将天文方位角归化为大地方位角---起始方位角
在布设国家天文大地网时,为了控制三角网中方位角传算误差的积累,要求在一等三角锁的两端和中央,以及二等网的中间等处,都要在起始边的两个端点上,用天文观测的方法测定它们的天文经度![]() 是以测站的垂线为依据的,因此必须将它归算至椭球面以测站点相应的法线为依据的大地方位角A,这种归算又称起始方位角的归算。将天文方位角归化为大地方位角的计算公式是:
是以测站的垂线为依据的,因此必须将它归算至椭球面以测站点相应的法线为依据的大地方位角A,这种归算又称起始方位角的归算。将天文方位角归化为大地方位角的计算公式是:
![]() (7-94)
(7-94)
式中A为测站点到照准点的大地方位角,α为测站点处相应方向的天文方位角;L为测站点的大地经度;![]() 为垂线偏差改正数,按(7-86)计算。当照准点目标高度不大时,天顶距Z接近于900时,可勿略不计,因此上式可写为:
为垂线偏差改正数,按(7-86)计算。当照准点目标高度不大时,天顶距Z接近于900时,可勿略不计,因此上式可写为:
![]() (7-95)
(7-95)
该式又称为拉普拉斯方程式,大地方位角又叫拉普拉斯方位角,在三角点上观测天文经度、天文纬度时,该点叫拉普拉斯点。
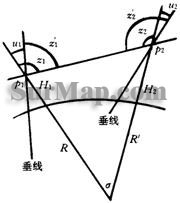 7.6.3观测天顶距受垂线偏差影响的改正
7.6.3观测天顶距受垂线偏差影响的改正
用三角高程方法测定相邻三角点的大地高差时,在三角点P1和P2上必须进行天顶距的观测,设观测值分别为![]() 计算大地高差,因此对观测天顶距应加垂线偏差改正数。垂线偏差在测线的分量为
计算大地高差,因此对观测天顶距应加垂线偏差改正数。垂线偏差在测线的分量为
![]()
由图可知,大地天顶距![]() 的计算公式为
的计算公式为
![]() (7-96
(7-96
式中A为测站点至照准点的大地方位角。
利用上式公式计算出的大地天顶距Z可用于计算高差,此高差称为大地高差。但三角高程测量的精度是有限的,若提高其计算精度,必须设法克服大气折光的影响,同时要在天顶观测值中引入垂线偏差改正数。
