3.15偏心观测与归心改正
标石中心B，仪器中心Y，照准点中心T
3.15.1测站点归心改正
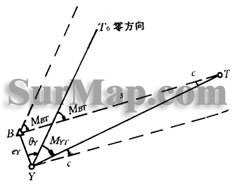
1几个名词
测站偏心：仪器中心Y偏离标石中心B
测站归心改正：把测站偏心时观测的方向值
测站归心改正数c: 
测站偏心距：
测站偏心角：
测站偏心元素：
2公式
(3-100)
3.15.2照准点归心改正
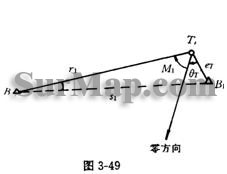
1几个名词
照准点偏心：照准点中心T1偏离标石中心B1
照准点归心改正：把照准点偏心时测得的方向值
照准点归心改正数r1 
照准点偏心距：
照准点偏心角：
照准点偏心元素:
2公式
(3-101)
3.15.3一测站同时受到两种偏心的影响
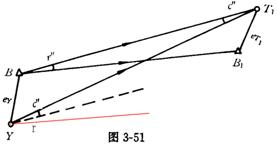
3.15.4归心元素的测定方法
3.15.5归心元素测定精度的探讨
1计算归心改正数必须精度
）
这样就提出归心元素测定精度必须保证c,r的误差不影响不降低水平角（方向）观测的精度，这就是规定归心元素测定精度的出发点。
(3-102)
一般取
(1)
要求 
(3-103)
如果将(3-103)代入(1)有
由此可以看出，当满足(3-103)时，就能保证方向观测值的精度基本上与测站平差后方向观测值的精度相同，也就是说，并没有因加了归心改正数而降低了方向观测值的精度。
一般
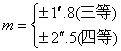
代入(3-103)得，
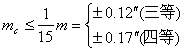(3-105)
这就是计算归心改正的必须精度。
2测定e的必须精度
⑴求
(3-100)对e微分，并将微分改写成中误差，再考虑
的数值最大
(3-108)
(3-108)式表明，测定e的精度与e本身无关，只随边长s而变化，边长愈短，测定e的精度要求愈高。
根据(3-105)确定的
⑵求示误三角形与的关系
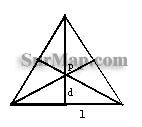p为最后决定的投影点位置。
如果认为d是投影点在交会方向线上的横向误差，且纵、横向误差等影响，则投影点在任一方向的位置误差为
，
偏心距是两点之间的距离，所以，
或 
(3-114)
⑶讨论
由(3-105)和(3-108)可得
(3-110)
代入(3-114)得
(2)
下面分两种情况讨论
第一种是国家等级三角网情况，ms基本为一常数，可取ms=14
（秒公里）,分别代入(3-110)和(2)得
(3-112)
由于标石中心和仪器中心易于投影，所以示误三角形边长不得超过5mm,而照准点……允许不大于10mm.
第二种城市、工程控制网情况，
IV等， s=2km, 
,
这个结论说明，对于边较短的城市、工程控制网，不能按国家规范的要求做，要十分注意投影的质量，最好不要有偏心观测。
3测定偏心角θ的必要精度
⑴求
(3-100)对θ微分，并将微分改写成中误差，再考虑的数值最大
(3)
(3-105)可写为
（3-113）
表明当边长愈短或偏心距愈大时，对偏心角测定的精度要求愈高。
| 偏心距
e |
三等s=8km,
|
四等S=6km,
|
四等S=2km,
|
| 0.1m | 2040/ | 2050/ | 0056/40// |
| 0.2m | 1020/ | 1025/ | 0028/20// |
| 0.3m | 0053/20// | 0056/40// | 0018/53// |
| 0.4m | 0040/00// | 0042/30// | 0014/10// |
| 0.5m | 0032/00// | 0034/00// | 0011/20// |
| 0.6m | 0026/40// | 0028/20// | 0009/27// |
当e<0.3m时，一般用投影法，当边长较短时也要用15/的量角器量取。当e>0.3时，投影用纸没有那么大，要求测定θ的精度也高，只好直接测定。
⑵在投影时，检查角的描绘值与观测值之差，在一定程度上代表了θ角的投影中误差，因此检查角的最大误差也就是检查角的描绘值与观测值之差的限差，
以e=0.3m代入上式得Δ=10.7，规范规定不得超过20，这是考虑国家等级边长较长；对于边长较短的工程网，要大大严于此要求。
4对边长概略值的要求
（3-100）对s微分，并将微分改写成中误差，再考虑的数值最大
(4)
| 偏心距
e |
三等s=8km,
|
四等S=6km,
|
四等S=2km,
|
| 0.1m | 372m | 296m | 33m |
| 0.2m | 186m | 148m | 16m |
| 0.3m | 124m | 99m | 11m |
| 0.4m | 93m | 74m | 8.2m |
| 0.5m | 74m | 59m | 6.6m |
| 0.6m | 62m | 49m | 5.5m |
上式表明边长愈短或偏心距愈大时，对边长概略值的要求愈高。
可见边长概略值很容易达到。