由一定半径的圆弧构成的曲线,称为圆曲线。在路线中线由一直线方向转变为另一直线方向时,或由一坡度转变为另一坡度时,为保证运行安全,一般在水平方向和竖直方向均设置一定半径的圆曲线。下面介绍水平方向上圆曲线的测设方法。
(一) 圆曲线的要素及其计算
如图 10-63 所示, A 为某道路中线的起点,其里程为 0+000 ,道路中线由 AJ D 1 方向转变为另一直线方向 J D 1 - JD 2 , 为了行车安全,需在其间设置平面圆曲线“ ZY - QZ - YZ ”,其名称和常用符号结合图 10-63 介绍如下:
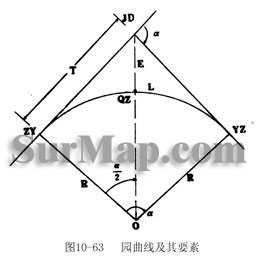
R ——圆曲线半径,在测设中根据路线等级及地形条件选定;
α ——转向角,由设计图纸提供,或在路线定测时实测;
JD ——转向点,或称交点,根据工程的设计条件测设;
ZY ——直圆点,圆曲线的起点;
QZ ——曲中点,圆曲线的中点;
YZ ——圆直点,圆曲线的终点;
T ——切线长, JD 至 ZY(YZ) 的直线距离;
L ——曲线长, ZY 至 YZ 的弧长;
E ——外矢距, JD 至 QZ 的直线距离;
q ——切曲差,两倍切线长与曲线长之差。
通常,把 T 、 L 、 E 、 q 四元素称为圆曲线要素。把 ZY 、 QZ 、 YZ 三点称为圆曲线主点。由图 10-64 可知,各要素的计算公式如下:
 ( 10-25 )
( 10-25 )
(二) 圆曲线主点桩号的计算
在线路测量中,曲线段的桩号是按曲线传递的,若已求出圆曲线要素及交点 JD 的桩号,则计算圆曲线主点桩号的一般公式如下:
 ( 10-26 )
( 10-26 )
主点桩号的检核,可用切曲差 q 来验算,其公式为:
![]()
(三) 圆曲线主点的放样方法
求出圆曲线要素之后,可按下述步骤测设圆曲线主点:
1. 将经纬仪安置于交点 J D 1 上(见图 10-63 ),分别瞄准起点 A 和交点 J D 2 ,从 J D 1 起沿切线方向用钢尺测设切线长 T ,在地面上分别标定出曲线起点 ZY 和曲线终点 YZ 。
2. 经纬仪在 J D1 不动,以 J D2 为零方向,盘左、盘右两次测设水平角 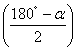 ,取平均位置作为该角之分角线方向,并沿分角线方向从 JD1 起测设外矢距 E ,在地面上标定出曲线中点 QZ 。
,取平均位置作为该角之分角线方向,并沿分角线方向从 JD1 起测设外矢距 E ,在地面上标定出曲线中点 QZ 。
圆曲线主点对整条曲线起着控制作用,测设正确与否,将直接影响曲线的详细放样。
(四) 圆曲线细部点的放样方法
在地形变化不大的地区,且曲线长 L < 40m 时,仅测设曲线三个主点已能满足道路施工要求。如果地形变化较大,曲线较长或半径较小(小于 150m ),仅测设主点就不能全面代表曲线的位置。这时,为了施工准确和方便,应在曲线上每隔一定距离测设一个细部点,并钉一木桩,此项工作称为圆曲线细部点放样,或称圆曲线的详细测设。有了这些细部点,就可以把曲线的形状和位置详细的表示出来。在实测中,一般规定: R ≥ 150m 时,曲线上每隔 20m 测设一个细部点; 150m > R > 50m 时,曲线上每隔 10m 测设一个细部点; R ≤ 50m 时,曲线上每隔 5m 测设一个细部点。
圆曲线细部点放样的方法较多,但在全站仪日益普及的今天,实际工作中比较实用且效率较高的测设方法仍能是直角坐标法与极坐标法。它是根据两个互相垂直的距离 x 、 y 的直角坐标定位原理来测设圆曲线细部点,故名直角坐标法。在地势平坦、便于测量的地方,采用本法较为迅速方便。通常先计算各点坐标,再到实地测设。
1 .坐标计算
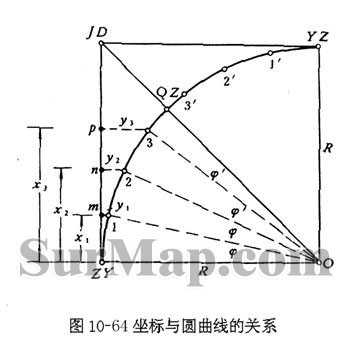
如图 10-64 ,本法是以圆曲线起点( ZY )或终点 (YZ) 为坐标原点,以切线为 x 轴,以过原点半径为 y 轴,当各细部点间弧长均为 K 时,则其所对应的圆心角 φ 按下式计算:
![]() (10-27)
(10-27)
弧长 K 所对应的弦长 S 按下式计算:
![]() (10-28)
(10-28)
各细部点平面直角坐标 x 、 y 按下式计算
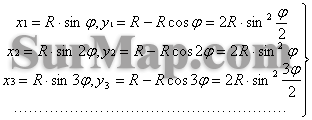 ( 10-29 )
( 10-29 )
弦弧差: 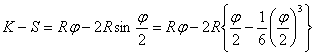
即 ![]() ( 10-30 )
( 10-30 )
2 .测设步骤
l 首先检核原放样的三个主点 ZY 、 QZ 、 YZ 的位置,若有错误,随时纠正。
l 参看图 10-65 ,沿切线 ZY - JD 方向测设 x1 , x2 , x3 ……,并在地面上标定出垂足 m 、 n 、 p ……
l 在垂足 m 、 n 、 p ……处用经纬仪、特制的直角尺或“勾股弦”法作切线的垂线,分别在各自的垂线上测设 y1 , y2 , y3 ……,以标定点 1 、点 2 、点 3 、……各细部点。
l 同法,从 YZ - JD 切线方向上测设圆曲线的另一半。
用 (10-31) 式计算得出的各细部点坐标( xi , yi )可以很容易地反算出极坐标放样的数据β i , Si ,从而可用全站仪放样各细部点位置,并且会有更高的工作效率。
