摘 要
由于空间科学的发展、进行大型特种精密科学实验以及各种现代化建设的需要,工程建筑物的规模越来越大,建筑物的结构和内部设施也越来越复杂。为了保证大型精密设备的安装和正常运行,不但对各种工艺构件间相互位置的精度要求越来越高,而且对测量的速度要求越来越快。现代科技的发展促进了工程测量学的发展,作为这门学科的扩展和延伸,出现了精密工程测量。精密工程测量的主要任务是解决各种大型和特种精密工程所提出的极高精度要求。 在大型特种精密建筑物中,最典型的工程建筑物要数高能离子加速器工程。 此外还有:大型核电站、高速磁悬浮、大型射电天文望远镜等等。这些大型特种精密工程的特点是: 由于它们的大型化和稀有性,耗资巨大,并且必须确保在极其安全可靠的状态下无故障、高效能的运行,因此它们的精度要求特别的高,绝对精度 达到毫米级别,相对测量精度达到1×。本文将以跨河为例来谈谈精密工程测量的这些特点。
关键词:精密工程测量;测量机器人;工程形变监测;专用仪器;测量软件;控制网布设;工程测量;相对精度;跨河水准
一、精密工程测量的定义和特点
工程测量分为普通工程测量和精密工程测量。仿照工程测量学的定义,精密工程测量主要是研究地球空间中具体几何实体的精密测量描绘和抽象几何实体的精密测设实现的理论、方法和技术。精密工程测量代表工程测量学的发展方向。所谓精密,顾名思义是精确严密。
精密工程测量的最大特点是要求的测量精度很高。精度这一概念包含的意义很广,分相对精度和绝对精度。相对精度又有两种,一种是一个观测量的精度与该观测量的比值,比值越小,相对精度越高,如边长的相对精度。但比值与观测量及其精度这两个量都有关,同样是1∶1 000 000 ,观测量是10 m和是10 km 时,精度分别为0.01 mm 和10 mm ,故有可比性较差的缺点;另一种是一点相对于另一点,特别是邻近点的精度,这种相对精度与基准无关,便于比较,但是各种组合太多,如有100 个点,每一个点就有99 个这样的相对精度。绝对精度也有两种,一是指一个观测量相对于其真值的精度,这一精度指标应用最多(下面所提精度,都指这种精度)。由于真值难求,通常用其最或是值代替。但这一绝对精度指标也有弊病,有时,它也与观测量的大小有关,如长度观测量。另一种是指一点相对于基准点的精度,该精度与基准有关,并且只能在相同基准下比较。
由于精度的含意较多,而且随测量技术的发展又在不断提高,有什么精度要求的测量才能称为精密工程测量就很难给出一个确切的定义。这里我们给出以下定义:凡是采用一般的、通用的测量仪器和方法不能满足工程对测量或测设精度要求的测量,统称精密工程测量。
大型工程、特种工程中并非所有的测量都是精密工程测量。因此,大型工程、特种工程不能与精密工程并列。但是,大型特种工程中一定包括一些或许多精密工程测量。3 维工业测量、工程变形监测中的许多测量也属于精密工程测量。就精度而言,在工业测量中,在设备的安装、检测和质量控制测量中,精度可能在计量级,如微米乃至纳米;在工程变形监测中,精度可能在亚毫米级;在工程控制网建立中,精度可能在毫米级。长、大隧道的横向贯通精度虽然在厘米、分米级,但对测量精度要求很高,仍属于精密工程测量。
精密工程测量的另一个特点是对测量的可靠性要求也很高,包括测量仪器的鉴定检核、测量标志的稳定、测量方法的严密、测量方案的优选、观测量之间的相互检查控制,以及严密的数据处理和对测量的质量检查控制以及监理等等。
二、精密工程测量研究的主要内容
精密工程测量的研究内容主要包括精密工程测量的理论、技术、方法、专用的仪器设备以及测量软件研发等方面。
精密工程测量的研究内容主要包括精密工程测量的理论、技术、方法、专用的仪器设备以及测量软件研发等方面。北方向等。对于工程而言,小范围要求在几何平面上进行设计施工放样,大范围有时要穿过好几个3度带,而且高差也较大,就必须作椭球面向平面的归化计算,作局部大地水准面的精化,以及换带和投影计算。归化、投影等改正计算误差必须小于测量误差。因而,工程基准面和局部坐标系的设计是精密工程测量的重要问题。
工程控制网在许多方面有别于国家大地测量控制网。网的优化设计、精度、可靠性、费用和灵敏度设计计算要求更加精细,如要求采用基于观测值内部可靠性的精密测量控制网模拟法优化设计、观测值多维粗差定位与定值和方差分量估计算法等。一般来说工程控制网的长短边相差悬殊,点之间高差也很大,GPS 和地面观测条件都较差(顶空障碍大,受旁折光和垂直折光影响等) ,这就要求对网作精心布设。同时还涉及GPS 边、地面边之间的精度匹配、地面边角测量精度匹配的影响。GPS 网、地面边角网以及混合网的布设问题涉及到测距三角高程测量、精密几何水准的选取以及对规范要求的理解等问题。GPS 网在很大程度上逐渐取代地面网,对于边长悬殊极大(从几十米到几十千米) 的工程控制网,用精密星历解算基线,精度也可达毫米级,但对于许多精密工程来说,不能采用单纯的GPS 网、GPS网与地面网、特别是与高精度测边相结合乃是最新的发展方向。
在精密工程测量特别是工程变形分析中涉及到数据处理理论和方法的研究。如非线性随机模型的参数估计、非参数估计和半参数估计理论。对于海量变形监测数据处理,要研究数据挖掘理论与方法,即要从大量的、模糊的和随机的各种数据源中,提取隐含在其中的有用信息和知识。统计分析、模糊数学、人工神经网络、分形几何以及小波理论等是数据挖掘的基础理论。分类、模糊聚类、关联分析、回归分析、时序分析、偏差分析以及预测分析等是数据挖掘的常用方法。其中,分类用于规则描述,并用这种描述来构造模型;模糊聚类是把数据按相似性分成类,发现数据的分布模式以及数据属性间的关系;关联分析是寻找数据中隐藏的关联网、关联规则和相关性;预测分析是利用大量的已有数据通过建模找出变化规律,由此对未来数据及特征进行预测等等。采用人工神经网络技术可用于大坝变形预报,用模糊数学理论处理观测误差,采用模糊聚类分析可对大坝的安全进行评判。在变形的几何分析和物理解释基础上,要研究变形预报的理论和方法,涉及系统论、控制论、信息论、突变论、协同论、小波、分形、混沌理论和耗散结构等许多非线性学科变形预报的系统论方法。主要有两种:一种是输入2输出模型法,即把变形体看作是一个具有非线性、耗散性、随机性、外界干扰不确定性等特点的复杂系统,各种外界影响因子为输入,而变形为输出,有回归分析法、时间序列法、卡尔曼滤波法和人工神经网络法等;另一种是动力学方程法,根据系统运动的物理规律建立确定的微分方程来描述系统的运动,在对系统受力和变形认识的基础上,用低阶、简化的,在数学上可求解和可分析的模型来模拟变形过程。
在精密工程测量仪器方面,多传感器集成测绘系统、激光跟踪仪、激光扫描仪、测量机器人、各种高精度GPS 接收机、电子全站仪、水准仪以及各种专用测量仪器,为精密测绘提供了技术保障。其中,激光扫描仪可对被测对象在不同位置扫描、建模并转换到CAD 成图,在土木工程、建筑监测、路桥设计、3 维建模、工业设计制造以及GIS 数据采集等方面有广阔的应用前景。车载、机载激光扫描测量将成为地面数据采集的主要手段。一种由测量小车、测量机器人、激光测距断面仪、激光扫描仪和轨距、轨道高差、轨道里程传感器组成的高速铁路轨道测量系统是一种典型的多传感器集成测量系统,可实现铁道轨道的自动化测量,轨道限界2 维断面测量和隧道3 维断面测量其轨距和轨道高差精度可达到0. 5 mm(图1) 。由GPS 接收机、激光测距仪组成的远程位移测量系统可实现无人值守的远距离遥控遥测遥传实时变形监测,可用于活动性滑坡临滑前的持续监测预报(图2) 。由各种专用监测仪器、现代大地测量仪器以及空对地观测仪器组成的立体监测系统,可实现对滑坡和各种工程建筑进行持续的自动监测和变形预报。

在现代测量中,软件的研发与测量仪器设备的研制具有同等重要的意义。精密工程测量的软件包括三大方面:与测量仪器或多传感器集成的测量系统相配套的随机软件;用于科研的科研型软件;面向广大用户的商品化通用软件。随机软件由厂商开发,如GPS 接收机的基线向量解算和网平差软件,电子全站仪的机载软件等,目前多已实现汉化,具有最常用的功能;科研型软件的专用性强,具有特殊的和高难的功能。一般来说使用较复杂,不易掌握。如用精密星历解算长基线的Gamit ,Berness 软件。用于精密工程控制网数据处理和平差计算的科研型软件除了具有一般的常用功能外,还具备以下功能:可作自由网平差或拟稳自由网平差;可对不同类型、不同精度观测值按不等权进行整体平差;可作距离改化、方向改化计算;能自动组成全部三角形并作计算闭合差和限差检验;自动组成测角、测边全部极条件,并计算其自由项及限值;自动计算坐标方位角、基线或测距边条件的自由项及其限值;还可以作观测值的可靠性因子(多余观测分量) 计算、边角权匹配计算、粗差检验及灵敏度分析等。
商用化通用软件的特点是功能强大,使用方便。下面介绍几个典型的商品化软件。
1. 现代精密工程测量控制网数据处理通用软件包Cosa - Win。可作任意网形(从导线、导线网到边角网、混合网、特殊网等) 、任意规模(未知点数从1~104) 、任意等级平面网、水准网或三角高程网的各种严密数据处理:观测值改化、概算、近似坐标、闭合差自动计算、粗差探测、方差分量估计、隧道贯通误差影响值计算、地面网和GPS 网优化设计、坐标转换、网图显绘、报表输出以及变形监测网的拟稳平差和变形分析等。
2. 精密GPS 控制网通用平差软件包(Cosa -GPS) 。可与各种GPS 接收机的基线向量软件接口,读入基线向量及其方差协方差,在WGS284 坐标系下进行3 维网的无约束平差,在高斯平面坐标系下进行2 维无约束平差、约束平差,与地面测边网联合平差,进行GPS 高程拟合。
3. 测量机器人变形监测软件包。具有工程管理、系统初始化、学习测量、自动测量、数据处理、数据查询、成果输出、工具、帮助等功能。该软件包安装在便携机上,便携机和测量机器人连接,用软件包控制测量机器人工作。以基点(测量机器人的位置)为基准,一已知点定向,另一已知点检查,根据极坐标原理,可获得各个测点的坐标。该法外业观测简单省时,效率高。如对某滑坡监测,常规方法外业观测需3 天,而采用该方法却不到2 小时。数据处理也实现了自动化。
4. 测量机器人控制网自动观测软件包。可实现工程管理、参数设置、测站设置、学习测量、自动观测和成果输出等功能。该软件包是直接植入测量机器人,实现测量机器人自动观测,进行设置和初始观测后,测量机器人就可按照设定的精度、测回数等进行全自动观测。这样可大大节省外业观测的时间和人力,如某滑坡监测网有15 个点,采用人工观测至少要15 天,而用测量机器人仅需5 天。还可与后续的软件相接,进行网平差。
三、精密工程测量的若干发展与应用
精密工程测量的发展也可概括为“四化”和“十六字”,所谓“四化”是:工程测量内外业作业的一体化,数据获取及其处理的自动化,测量过程控制和系统行为的智能化,测量成果和产品的数字化。“十六字”是: 连续、动态、遥测、实时、精确、可靠、快速、简便。
包含精密工程测量的典型工程非常多,如我国举世瞩目的长江三峡工程和其他的大型水利枢纽工程,长达30 km 多的杭州湾大桥、上海东海大桥以及其他特大桥梁工程,长18. 5 km 的秦岭隧道、长达85. 3 km 的大伙房引水隧道以及其他特长隧道工程,上海磁浮铁路、东方明珠塔和国家大剧院等特种工程,香港大佛工程,北京正负电子对撞机工程,大型大坝变形监测工程,高边坡和滑坡岩崩变形监测工程,大型设备的安装、检测和质量控制等都属于精密工程测量的范畴。
国外的典型大型工程、特种工程更是数不胜数, 单就大型粒子加速器而言,欧洲原子核研究中心的环形正负电子对撞机LEP , 整个工程位于直径8. 6 km、周长27 km 且深度达百米的地下环形隧道,布设有5 000 多块四极聚焦磁铁和两极弯转磁铁。瑞士的阿尔卑斯山隧道长57 km ,据报道其造价与我国的长江三峡工程相当。而建筑工程师梦寐以求的建造2 000 m 乃至更高的摩天大厦,都是对精密工程测量的挑战。
下面以应用精密三角高程测量进行跨河水准测量为例说明精密工程测量的应用。
四、应用精密三角高程测量进行跨河水准测量
当水准路线必须跨越江河或峡谷时,视线将超出常规水准的长度或前后视距相差很大,一方面水准尺读数的精度将会降低,另一方面水准仪t 角误差及大气折光的影响也会急剧增大。
当水准路线跨越江河,视线长度超过100 m 时,应根据视线长度和仪器设备情况,选择适当的跨河水准测量方法。
三角高程测量是测量高程的传统方法,以其快速、简便且能保证一定精度而深受测绘工作者喜爱。特别是近年来全站仪的发展提高了测角和测距的精度,目前全站仪测角精度达到+0.5" ,测距精度达到,同时自动化程度越来越高。自动全站仪能自动识别、跟踪和精确照准目标,大大提高了工作效率。因此,以全站仪代替水准仪进行高程测量,无疑具有明显的经济效益和社会效益。目前,三角高程测量己可以代替三四等跨河水准测量,但用于代替精密跨河水准测量仍处在研究阶段,已有不少文献就此进行研究,并得出了一些结论。
1. 正高高差计算及误差分析


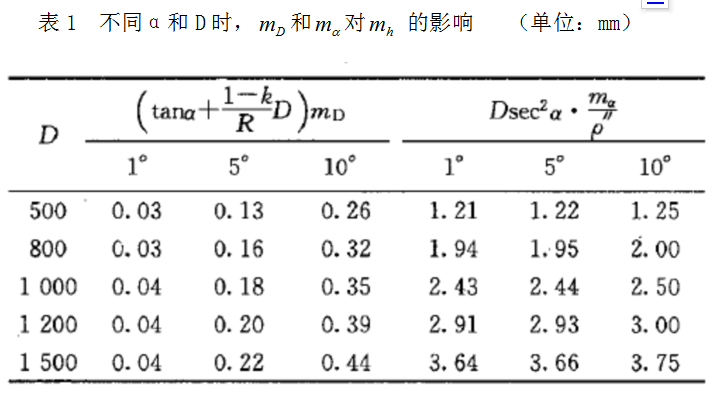
从表1中可以得出以下结论:
(1) 对的影响远远大于对的影响。可见,测角误差是三角高程测量的主要误差来源,因此要尽可能采用高精度的测角仪器,观测时要保证成像清晰稳定,并适当增加测回数。
(2)对的影响随角度增加的变化量较大,而随距离增加的变化量较小,因此观测角度不能超过一定范围。
(3)对的影响随角度增加的变化量较小,而随距离增加的变化量较大。因此跨河长度需控制在一定范围内,这就要求跨河点位尽量选择在河道狭窄处。
对于仪器和舰标量高中误差,按常规的方法量测仪器高和舰标高,精度很难满足要求,可以采用水准标尺读数法确定仪器高和胡标高,在测站通过全站仪观测水平视线在近标尺点上的标尺读数,根据两点间的己测水准高差计算仪器高。这种方法测定的仪器高比直接量取准确,精度可以达到0.1 mm。
大气折光影响也是三角高程测量的一项主要误差来源。在跨河三角高程测量时,大气折光对高差的影响具有一定的特殊性。跨河视线不仅通过地面,而且通过水面,由于地面和水面上空空气密度分布不均,形成了视线两端向上弯曲,中间向下弯曲的"U" 型曲线。故通过对向观测取平均值,可以消除一部分大气折光影响。如果观测是在同样情况下进行的,特别是同一时间内进行对向观测,则可以近似地假定对向观测的折光系数是相同的。
因此,为了削弱大气折光对三角高程测量的影响,凡是三等以上(含三等)三角高程测量的垂直角都应做到对向观测,最好是同时对向观测。
2. 跨河测距三角高程的精度估算
要测跨河的A 、B 点之间的高差,由于交通工具的限制,不便迅速搬站,必须采用2 台同样精度的全站仪和2 个同样的照准装置,进行对向观测,即先将仪器置于A 点, B 点安置反射棱镜,直接测定高差,再将仪器置于B 点, A 点安置反射棱镜,直接测定高差。然后取两高差的中数作为观测结果。仪器高通过水准标尺读数法获得,观测之前将2 个照准装置的棱镜高设置成相同的,边长垂直角均对向观测,垂直角观测6 测田,边长观测4 测回。观测使用TC2002 全站仪。

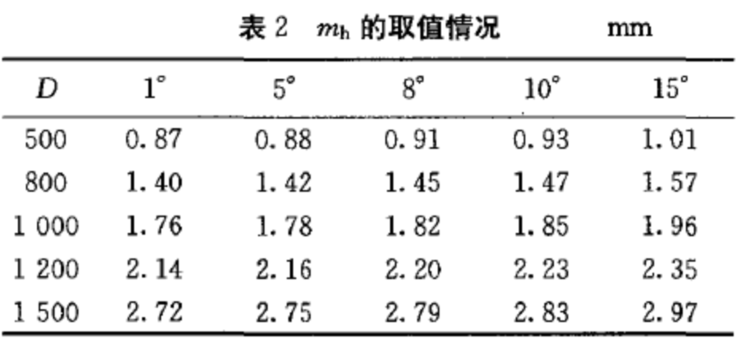
以2作为限差与国家二等水准测量限差比较,列于表3 。
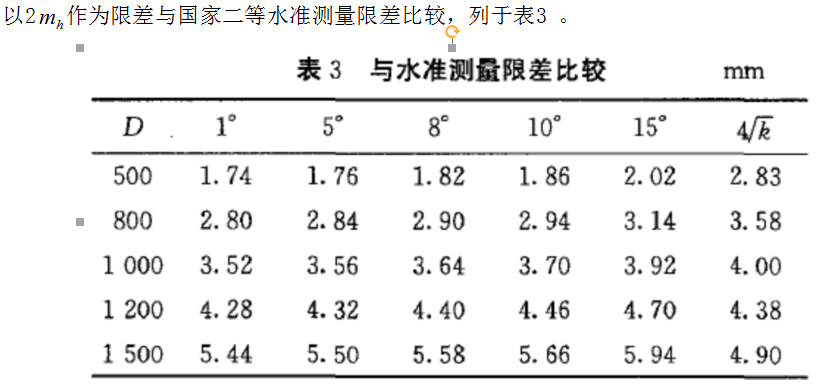
从表2 和表3 可以看出:
(1) 高差中误差随边长的增大而增大的量较大,因此,要控制边长保证精度。
(2) 利用精密三角高程测量实现跨河水准,跨河距离不能超过1 500 'm 。
(3) 当跨河距离不超过1 000 m 时,观测垂直角可以放宽到15°;距离小于1 200 m 时,垂直角控制在8°以内,满足二等水准测量的要求。
(4) 跨河水准用测距三角高程法时,其视线垂直角小于1°。
表3 表明,高差中误差随垂直角增大而增大的量甚小,在一定的边长范围内,即使垂直角超过规范要求仍能保证必要的精度,这对于跨河两岸高差较大的情况具有实际意义。
3. 自动化全站仪在跨河测量中的应用
自动化全站仪,也称测量机器人,是集自动目标识别、自动照准、自动测角、自动测距、自动跟踪目标及自动记录于一体的测量系统。测量机器人用于跨河测量具有以下优点:
(1) 测角精度很高,大大减小了由测角引起的误差。
(2) 具有自动目标识辨(Automatic TargetRecogni tion ,简称ATR) 功能,可以自动寻找并精确照准目标;允许在目标处使用普通的棱镜,而元需昂贵的特殊棱镜或添置电源等配件。
(3) 可以自动进行气象改正,克服气象代表性误差。
(4) 建立高精度的参考站,采用随时改正的测量方案,可以消除和减弱各种误差(外部的和仪器内部的)对测量结果的影响,大幅度地提高测量精度。现以TCA2003 自动化全站仪为例来说明。其测距精度,测角精度(一测回方向标准偏差)为±O. 5" ,若角度观测6 测固,取=±0.2" ,其他参数取值不变,和分别取不同的值时,高差中误差的取值情况,见表4 所列。
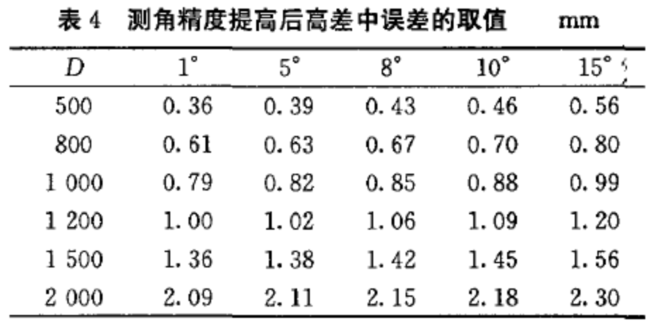
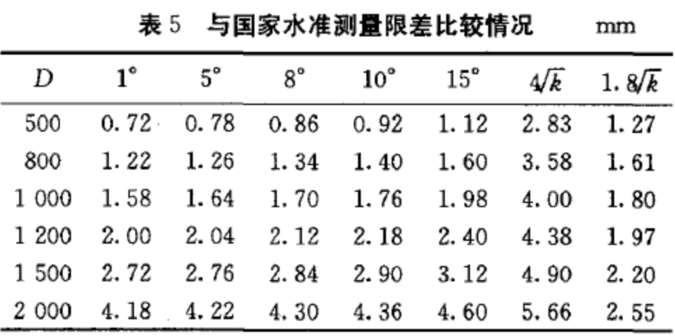
同样,以2为限差,与国家一二等水准测量限差比较列于表5 。不难看出,仅仅一项测角精度的提高,使得精密三角高程测量实现跨河水准更为容易。距离不超过2000 m 的情况下,可以达到国家二等水准测量的精度;跨河距离小于1000 m 时,垂直角控制在10°以内,可以满足国家一等水准测量的要求。
4. 总 结
本文对精密三角高程测量实现跨河水准的精度从理论上进行了分析,分析结果表明,在观测合理、处理方法得当的情况下,精密三角高程测量可以很容易实现国家二等水准测量。使用目前的高精度自动化全站仪,除了使操作更加便利外,可以提高三角高程测量的精度和实现更长距离的跨河测量,甚至有望实现跨江水准测量。
另外,对于短距离跨河测量,可以达到国家一等水准测量的精度。此外,实施跨河水准测量需要注意以下几点:
(1) 测角误差是高差误差的主要来源之一,因此要尽可能的采用高精度的测角仪器,观测时要保证成像清晰稳定,并增加测回数来提高测角精度。
(2) 垂直角在短距离测量高差中,影响高差值较大,在长距离测量高差中,影响高差值较小,所以在短距离测定高差中,应使仪器高与棱镜高的差距尽量缩小。
(3) 跨河水准测量受气象因素影响极大,因此观测应选在无风或微风天气进行,在气温变化较大时应停止观测。大气折光影响是个比较复杂的问题,本文参考了有关资料取为±0.01。
(4) 两岸同时对向观测,可以极大地提高精度,消除或减弱仪器高误差、大气折光差、地球曲率误差等多项误差。
(5) 随着跨河视线长度的增加,高差中误差急剧增大,因此在条件允许的情况下,要尽可能缩短跨河视线长度,将跨河水准点选在河道最窄处。
(6) 对向观测的2 个镜站设置同样标高,消除了标高误差。但观测时,要经常注意仪器及棱镜杆的圆水准器气泡是否居中,精度要求高时,应建造强制对中装置。
参考文献:
[1] 张正禄,吴栋材,杨 仁. 精密工程测量[M].北京:测绘出版社,1992.
[2] 张正禄. 工程测量学[M].武汉:武汉大学出版社,2005.
[3] 张松林, 张正禄, 罗年学. GPS平面控制网的模拟设计计算方法及其应用[J]. 武汉大学学报(信息科学版) ,2004 ,29 (8) :7112714.
[4] 张正禄,邓 勇,罗长林,等. 精密三角高程代替一等水准测量的研究[J] . 武汉大学学报(信息科学版) ,2006 , (1) :528.
[5] 张正禄,张松林,张 军,等. 特高精度水电站施工控制网分析与研究[J] . 大坝与安全,2002 (5) :17220.
[6] 刘祖强,杨 红,廖永龙. 三峡永久船闸建筑物变形特性分析[J] . 水电站自动化与大坝观测. 2005 ,9 (2) :59263.
[7] 孔祥元,梅是义.控制测量学(上册) [MJ. 武汉:武汉大学出版社, 2001: 254-260.
[8] GB 12897-1991 ,国家一二等水准测量规范[5].
[9] 周蕴.全站仪在桥梁高程控制测量中的应用及精度分析[J].中州大学学报, 2005 , 22(2): 107-109.
[10] 周西振,张锋强.精密跨河水准测量中大气垂直折光问题的探讨[J].地矿测绘, 2004 , 20( 1) : 18-20.
[11] 周水渠.精密三角高程测量代替二等水准测量的尝试[J].测绘信息与工程, 1999 , (3):25-29.
[12] 范百兴,夏治国.全站仪实施跨河水准测量及其精度分析[J].测绘工程,2004,13 (1) :41-43.
[13] 毛黎虎,王力.精密三角高程测量的精度分析[J].大坝与安全, 2004 (增刊): 63-67.
