要注意了,工程测量的坐标系和数学坐标系在定义上是有区别的,因此在计算公式上也有区别。定义的区别如下图:
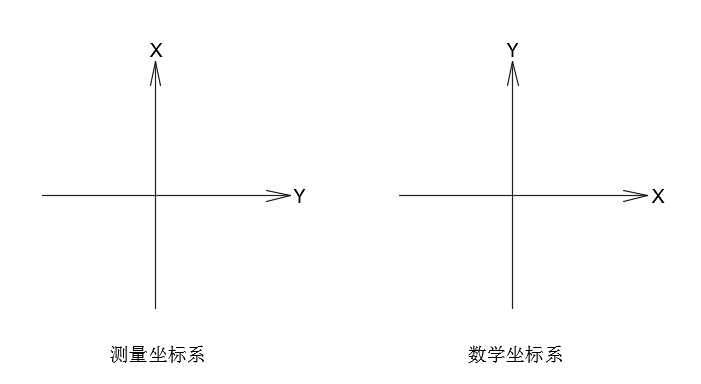
为啥这样定义?很难找到结果,就当约定俗成吧。除非你某一天能把它约定回来,不然咱还是遵守吧。
这个定义很坑,如果直接绘制在CAD里,左右会和实际相反,我们在将测量坐标绘入CAD时,只好将xy交换后绘图,这样绘制的图形才和实际相吻合。
坐标方位角
你除了知道坐标(x,y)之外,还有一个重要的东东要知道,不知道这个东东,你的工程测量只能算门外汉。嗯,那就是坐标方位角。
无图无真相啊,咱先看一张图。
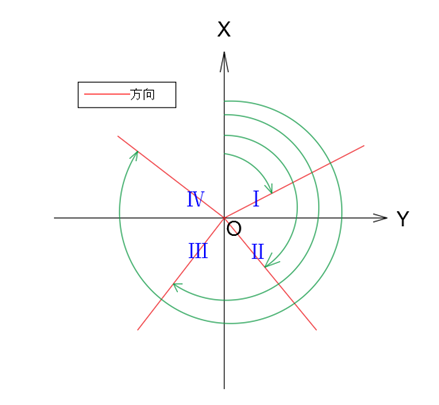
坐标方位角仅指一个方向,其值等于将坐标系原点平移至该方向起点,坐标零方向顺时针旋转到该方向的角度。
是不是还是难以理解?脑子里放一个线段,把测量坐标系的图移过去,原点与一个端点重合,从x方向开始想象有一条线顺时针旋转到与线段重合,旋转的角度就是与原点重合的点到另一点的方位角的值。
方位角的取值范围:0-360度,一般没有360度的方位角,因为到360度时又记为0度。
还有一个简便计算的特征:A到B的方位角=B到A的方位角+180度。这个特征在坐标推算时会用到的。
在工程测量坐标系里,一般你需要掌握以下三种计算:
坐标正算
坐标正算是指已知起算点的坐标及至目标点的距离和方位角,计算目标点的坐标。看一下图更容易理解。
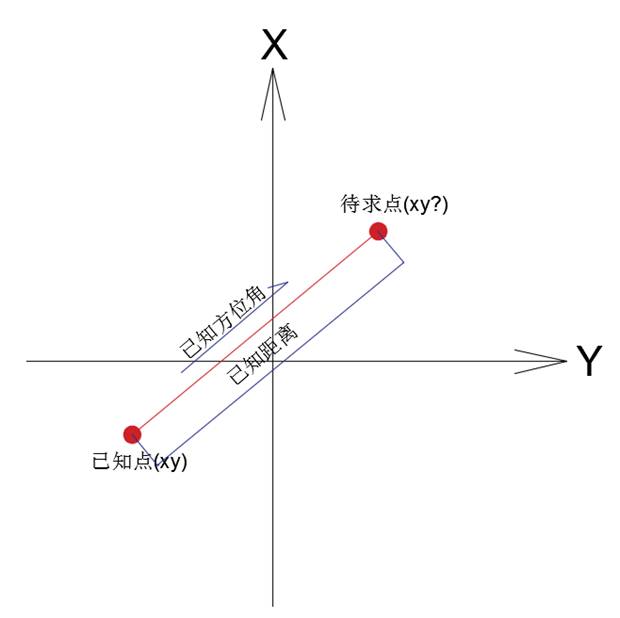
公式很简单:
X=x+s*cosF
Y=y+s*sinF
XY:待求点的xy;
x:已知点的xy;
s,F:已知点到待求点的距离和方位角。
坐标反算
坐标反算可以看作是坐标正算的逆运算,指已知起算点和目标点的坐标,计算起算点到目标点的距离和方位角。再看一张图:
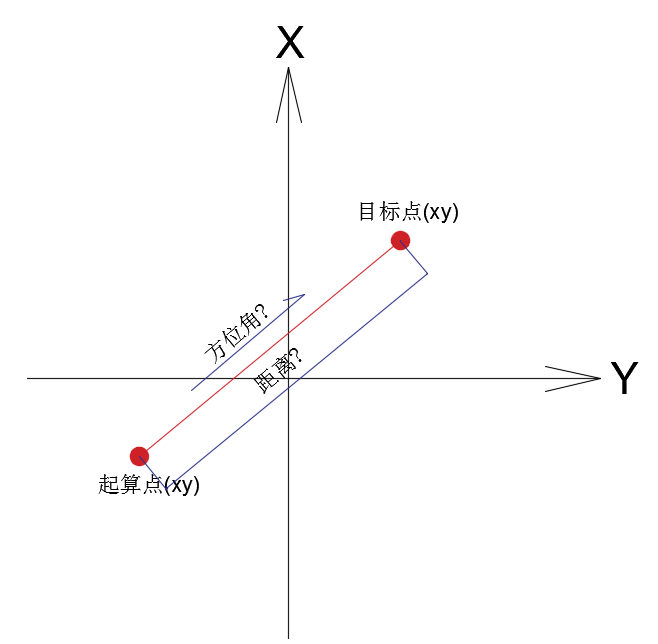
距离的计算相对简单:s=sqrt((x1-x2)^2+(y1-y2)^2))
sqrt:开算术平方根;
^:乘方的运算符号。
方位角的计算要稍复杂一点,其实也很简单。
先计算一个角度值:F=atan((y2-y1)/(x2-x1)),如果F为负,加360度即可。然后判断一下x2是否比X1小,如果小,F则加180度,否则不变。
atan:反正切。
鄙视一下:如果x2=x1,上面的公式还能用吗?这时F=90度,判断跟上面相同。
坐标变换
这个点比较难,要用到高中的数学知识。如果你具备高中及以上学历,就继续看下去吧。
坐标变换是指将一个坐标系里的坐标变换到另一个坐标系里,这在工程测量中常常用到,且可能带来想不到便宜效果。
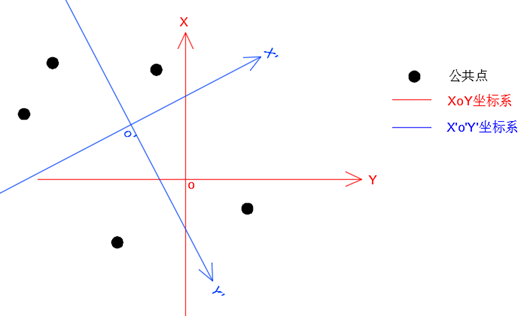
先看一个数学公式:
x2=x1cosα+y1sinα+A
y2=y1cosα-x1sinα+B
x1,y1:第一个坐标系的xy;
x2,y2:第二个坐标系的xy;
α:坐标系的旋转角;
A,B:坐标原点的平移值。
这就是初等数学里坐标系的旋转和平移公式,放到工程测量里面来,多了一些测量的概念,当然如果简单应用,跟初等数学并没有区别。
在实际的工作中,并没有现成的旋转角和平移值供我们使用,因此利用公式直接计算会很困难。肿么办呢?我们只有利用公共点计算旋转角和平移值,从而解算其他未知点。所谓公共点,是指该点同时具有两个坐标系的坐标,在实际中很容易根据定义或计算获得。
现在我们已知两个公共点进行转换公式推导:
假定A坐标系两点坐标为(x1,y1)(x2,y2),与之对应的B坐标系坐标为(x11,y11)(x21,y21)
令 a = x21 - x11 : b = y21 - y11 : c = x2 - x1 : d = y2 - y1
如果 c ^ 2 + d ^ 2=0,则转换无效。否则进行转换计算:
令 u = (a * c + b * d) / (c ^ 2 + d ^ 2) v = (a * d - b * c) / (c ^ 2 + d ^ 2) w = x11 - x1 * u - y1 * v : z = y11 + x1 * v - y1 * u
已知A坐标系一点坐标(yizhix,yizhiy),计算该点在B坐标的坐标(x,y)
x = yizhix * u + yizhiy * v + w
y = (-1) * yizhix * v + yizhiy * u + z
真的很简单,这在日常工地上已经足够使用了!
