依据<<建筑施工计算手册>>。
一、计算原理:
弹性地基基础上大体积混凝土基础或结构各降温阶段综合最大温度收缩拉应力，按下式
计算：
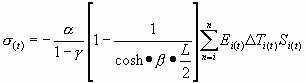
降温时，混凝土的抗裂安全度应满足下式要求：
式中 
(t)──各龄期混凝土基础所承受的温度应力(N/mm2)；
──混凝土线膨胀系数，取1.0×10-5；
──混凝土泊松比，当为双向受力时，取0.15；
Ei(t)──各龄期综合温差的弹性模量(N/mm2)；
△Ti(t)──各龄期综合温差（℃）；均以负值代入；
Si(t)──各龄期混凝土松弛系数；
cosh──双曲余弦函数；
──约束状态影响系数，按下式计算：
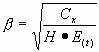
H──大体积混凝土基础式结构的厚度(mm)；
Cx──地基水平阻力系数(地基水平剪切刚度)(N/mm2)；
L──基础或结构底板长度(mm)；
K──抗裂安全度，取1.15；
ft──混凝土抗拉强度设计值(N/mm2)。
二、计算:
(1) 计算各龄期混凝土收缩值及收缩当量温差
取
y0=3.24×104, 则1dM1=1.42； M2=0.93； M3=0.70； M4=0.95； 收缩值为:
y0×M1×M2……×M10(1-e-0.01×1)=0.028×10-4
1d收缩当量温差为:
Ty(1)==0.28℃
同样由计算得:
εy(2)=0.056×10ˉ Ty(2)=0.56℃
εy(3)=0.084×10ˉ Ty(3)=0.84℃
(2) 计算各龄期混凝土综合温差及总温差
2d综合温差为:
T(2)=T(1)-T(2)+Ty(2)-Ty(1)=-1.72℃
同样由计算得：
T(3)=-1.72℃
(3) 计算各龄期混凝土弹性模量
1d弹性模量:
E(1)=Ec(1-e-0.09×1)=0.219×104N/mm2
同样由计算得:
E(2)=0.42×10N/mm
E(3)=0.603×10N/mm
(4) 各龄期混凝土松弛系数
根据实际经验数据荷载持续时间t,按下列数值取用:
S(1)=0.062;
S(2)=0.124;
S(3)=0.186;
(5) 最大拉应力计算
取 =0.15； Cx=0.02；
H=2500mm； L=90800mm。
根据公式计算各阶段的温差引起的应力
1) 2d (第一阶段）:即第1d到第2d温差引起的的应力：
由公式:
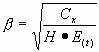
得：
=0.4364×10-4
再由公式:
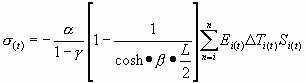
得：
(2)=-0.008N/mm2
同样由计算得：
2) 3d:即第2d到第3d温差引起的的应力：
(3)=-0.014N/mm
3) 总降温产生的最大温度拉应力:
(3)=-0.022N/mm2
混凝土抗拉强度设计值取0.4N/mm2,则抗裂缝安全度:
K=0.4/-0.022=-18.18<1.15 不满足抗裂条件