摘要:以BASE试件为基础设计3个具有不同长细比的ZG试件并进行了非线性有限元分析,采用了在钢管和混凝土之间加入粘接单元的方法。柱长细比是方钢管混凝土柱设计的主要影响因素,长细比可适当减小,柱长细比越大,柱承载力越低。在方钢管的底部和底角部存在应力集中现象,应力集中区域大约在柱高1/3范围内,对方钢管的底部应加大刚度,柱底角部应加强施焊。混凝土压碎破坏发生在柱底部,在管内混凝土的施工过程中,要保证混凝土柱底浇注密实。本文的研究结论对今后方钢管混凝土柱的设计和施工具有一定的指导意义。
关键词:方钢管混凝土柱,长细比,有限元
1 引言
方钢管混凝土的研究开展的较晚,各方面的理论还不够成熟和完善,以往的研究主要集中在试验研究上,本文采用有限元分析对方钢管混凝土柱的设计和施工提出合理建议,克服试验的不足。考虑到钢管混凝土是由钢管和混凝土两种不同材料所组成,混凝土和钢管之间有相对滑移,引入一种能反映钢管和混凝土两者间界面性能的单元----粘结单元,它能比较真实地反映方钢管混凝土柱的受力性能。
2 有限元模型的建立
本文模拟框架结构中间层的中柱,截取了方钢管混凝土柱从梁顶面到柱反弯点处的部分为研究对象。为了深入分析钢管混凝土柱的受力性能,充分考虑我国有关规范的规定,依据常见的工程实例设计了4个试件,采用大型商用有限元软件ANSYS对其受力性能进行了非线性有限元模拟。
2.1模型的几何尺寸
为了研究长细比对方钢管混凝土柱的受力性能影响,以BASE试件为基础,设计了ZG系列试件,详细尺寸见表1。
表1 试件尺寸明细表
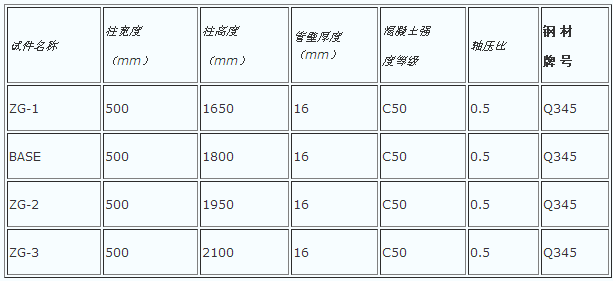
注:ZG-1(2、 3):Z代表柱子,G代表高度,1、2、3分别代表柱高度为1650mm、1950mm、2100mm。
2.2单元的选取
在ANSYS中用solid65单元[1-3]来模拟混凝土的材料性质,该单元为三维钢筋混凝土实体。钢管壁采用八节点六面体单元Solid45。
2.3 材料模型的确定
混凝土等级C50,弹性模量Ec=3.45×104N/mm2,泊松比μc=0.2;钢材认为是理想的各向同性的弹性材料,选用Q345,弹性模量Es=2.06 ×105N/mm2,泊松比μc=0.3。钢的应力---应变关系的计算模型取双折线弹性强化模型。
2.4 加载制度、约束情况
柱底固定,柱顶不加约束,先加柱顶竖向荷载N,再加柱顶水平荷载P。荷载的施加方式:柱顶轴力N以面荷载的形式施加在柱顶面S上;柱顶水平力P以位移形式施加,加载前先将S面上是所有节点的X向位移耦合在一个关键点上(见图1),施加的位移只需加在此藕合点的X向上。
3. ZY系列试件有限元计算结果及分析
方钢管混凝土柱的长细比为:
L—方钢管混凝土柱的计算长度;B—方钢管横截面外边长。
方钢管混凝土柱的长细比值见表2。
表2 柱长细比值

3.1荷载-位移曲线分析
柱长细比对荷载-位移曲线影响比较显著。随着柱长细比的增加,构件无论在弹性阶段还是在非线性强化阶段,其刚度均有所降低,承载能力也有所下降,而且下降的幅度较大。因为方钢管混凝土柱的长细比越大,柱越容易发生失稳,使柱承载力降低。
3.2混凝土裂缝分析
有限元计算ZG系列试件破坏时混凝土裂缝如图3所示:
3.1 ZG-1混凝土裂缝图 3.2 BASE混凝土裂缝图 3.3 ZG-2混凝土裂缝图 3.4 ZG-3混凝土裂缝图
ZG系列试件破坏时混凝土的裂缝集中在柱底部,特别在柱底角部混凝土的裂缝更加严重,并且都出现了贯通裂缝,导致混凝土被压碎。
随着柱长细比的增加,柱底混凝土的裂缝增多,特别柱底角部裂缝开始增多,裂缝逐渐连接并贯通,出现了贯通裂缝,贯通的裂缝将试件分裂成若干小柱,造成混凝土过早被压碎,柱的承载力降低。因此在管内混凝土的施工过程中,要注意柱底部和柱底角部的混凝土浇筑质量,保证混凝土振捣密实,确保工程质量。
3.3管内混凝土轴向应力云图分布分析
有限元计算ZG系列试件破坏时混凝土轴向应力云图如图4所示:

4.1 ZG-1混凝土应力云图 4.2 BASE混凝土应力云图 4.3 ZG-2混凝土应力云图 4.4 ZG-3混凝土应力云图
ZG系列试件破坏时,混凝土外表面的底部和中上部局部区域轴向压应力较大,最大轴向压应力超过了混凝土的抗压强度,导致混凝土被压碎。由于钢管和混凝土是由两种力学性质很不同的材料组成的,而且尺度相差很大,钢管和混凝土的弹性模量又不同,它们在轴向荷载和水平荷载作用下,出现相对滑移,它们之间产生的摩擦力和粘结力使得混凝土外表面大部分区域出现了轴向拉应力,但拉应力值较小,而混凝土内部则出现轴向压应力。
随着柱长细比的增加,混凝土柱底角部和柱中上部局部区域的最大压应力范围增大,混凝土内部的轴向压应力值随着柱长细比的增加而增大,使混凝土过早开裂,柱的承载力降低。
在管内混凝土的施工过程中,要注意柱底部和柱底角部、柱中上部的混凝土浇筑质量,保证混凝土振捣密实,确保工程质量。
3.4钢管的Mises应力分析
有限元计算ZG系列试件破坏时钢管的Mises应力图如图5所示:
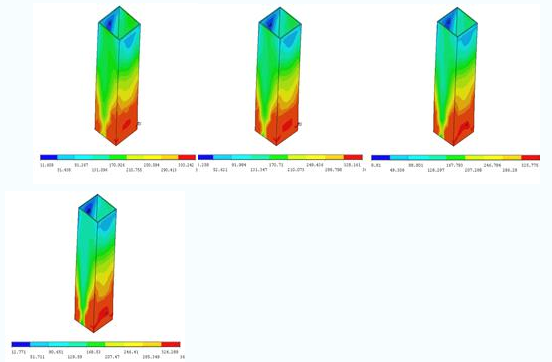
5.1 ZG-1钢管Mises应力 5.2 BASE钢管Mises应力 5.3 ZG-2钢管Mises应力 5.4 ZG-3钢管Mises应力
ZG系列试件破坏时,钢管的高应力区域集中在钢管的柱底部,特别在钢管底角部应力集中现象更为严重,柱的反弯点附近应力最小,钢管的柱底部和底角部应力最大,超过了钢材的屈服强度,进入塑性变形阶段,而钢管中间大部分区域应力较小。
随着柱长细比的增加,钢管柱底部、柱底角部的高应力区域范围增大,但最大应力值稍有减小,减小的幅度很小。在方钢管混凝土柱底部和角部会造成应力集中现象,因此对方钢管混凝土柱的底部应加大刚度,角部应加强施焊。
3.5测点和路径分析
在各试件中取4个测点,测点 1、2位于钢管外表面底部角点处,测点 3位于钢管外表面顶部角点处,测点 4 位于测点 1、3连线的中点处。连接测点1、2形成路径1,连接测点1、3形成路径2,连接点3、5形成路径3,如图6所示:
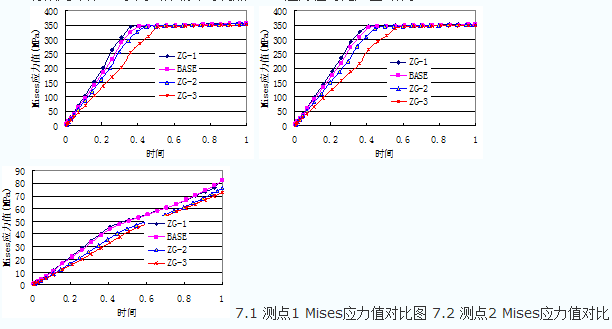
有限元计算ZG系列试件破坏时测点Mises应力值对比如图7所示:
图7看出:测点 1、2 的应力值最大,测点3的应力值最小。
从测点 1、2 Mises应力值对比图看出:改变柱长细比对测点 1、2的Mises应力值影响较小,在弹性阶段随着柱长细比的增加,Mises应力值减小,但减小的幅度较小,对ZG-3试件Mises应力值减小的幅度较大,进入塑性阶段四条曲线几乎重合,钢管均达到了屈服强度。随着时间的推移,应力曲线在弹性阶段上升较快,进入塑性阶段后变化趋势较为平缓。
从测点 3 Mises应力值对比图看出:改变柱长细比对测点 3的Mises应力值影响较小。随着柱长细比的增加,测点 3 的应力值减小,但减小的幅度很小,对ZG-1、BASE试件几乎没有影响,两条曲线几乎重合。随着时间的延长,测点 3 的应力曲线呈上升的趋势,各测点的应力值均远未达到屈服强度。
有限元计算方钢管混凝土柱ZG系列试件破坏时路径Mises应力值对比如图8所示:
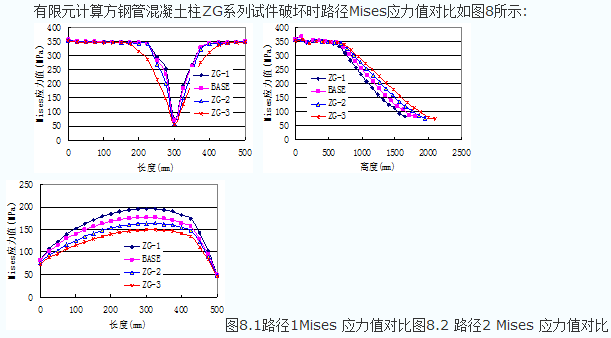
图8看出:路径1、2上应力集中区域钢管达到了屈服,而路径3上钢管均未达到屈服。
从路径1Mises 应力值对比图看出:随着柱长细比的增加,应力曲线的突变点值大小和位置几乎没有变化。在上升和下降阶段,随着柱长细比的增加,应力值减小。应力曲线先变化趋势较为平缓,后来下降,再上升,最后又变化趋势较为平缓。
从路径2 Mises 应力值对比图看出:在柱高度660mm内,应力值差别很小,四条曲线几乎重合,当柱高度超过660mm以后,应力值随着柱长细比的增加而增大。但应力曲线总体呈下降趋势,应力集中区域大约在柱高1/3范围内。
从路径3 Mises 应力值对比图看出:随着柱长细比的增加,Mises 应力值减小,到了长度425mm以后,Mises 应力值减小的幅度降低。
4 结论
长细比可适当减小,柱长细比越大,柱承载力越低。在方钢管的底部和柱底角部存在应力集中现象,应力集中区域大约在柱高1/3范围内,因此对方钢管的底部应加大刚度,柱底角部应加强施焊。混凝土压碎破坏发生在柱底部,在管内混凝土的施工过程中,要保证混凝土柱底浇注密实,确保工程质量。本文的研究结论对今后方钢管混凝土柱的设计和施工具有一定的指导意义。
参考文献
[1]ANSYS建模与网格划分.ANSYS中国.2001,1.
[2]ANSYS高级操作手册.ANSYS中国.2001,1.
[3]赵经文,王宏钰结构有限元分析(第二版).北京:科学出版社.2001.
