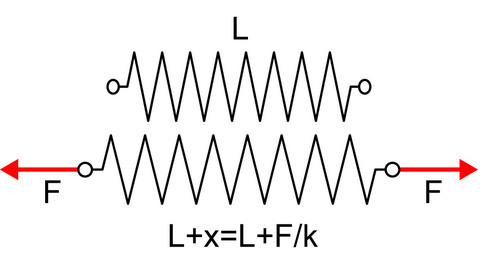
如果您还记得高中物理的大部分内容,那么您就知道有一个东西叫做「弹簧系数」。所谓的弹簧系数,其实就是弹簧的受力与弹簧的变形的比值,在结构工程里,这个比值也就是所谓的刚度。比如说我们上面这个弹簧,本来的长度是 L,我施加了一个大小为 F 的拉力,弹簧被拉长了,拉长之后的长度变成了 L+x,这其中的增加的长度 x 等于 F 除以弹簧系数 k。这也就是高中物理的 F= kx。
如果您还记得高中物理的大部分内容,那么您就知道有一个东西叫做「弹簧系数」。所谓的弹簧系数,其实就是弹簧的受力与弹簧的变形的比值,在结构工程里,这个比值也就是所谓的刚度。比如说我们上面这个弹簧,本来的长度是 L,我施加了一个大小为 F 的拉力,弹簧被拉长了,拉长之后的长度变成了 L+x,这其中的增加的长度 x 等于 F 除以弹簧系数 k。这也就是高中物理的 F= kx。
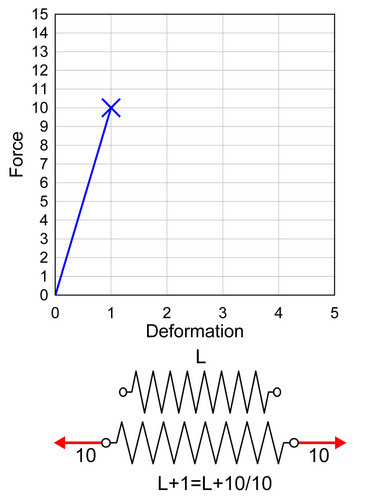
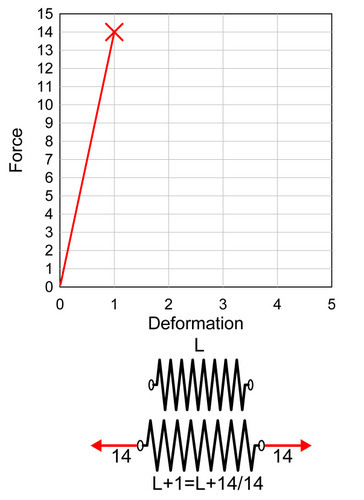
当然,我们也知道,弹簧并不是无限结实的,也就是说,弹簧不能被无限拉伸。大家也肯定都有拉断橡皮筋或者弹簧的亲身感受。当橡皮筋被拉长到一定程度的时候,突然啪的一声就断了。我们把整个拉长过程的变形和受力画成图形,当弹簧断裂的时候,最大的变形是 1,与之对应的最大的受力是10。也就是说,弹簧受力过程在受力变形的图形中是一条直线,这条直线的斜率就是弹簧系数 k,这其实就是 F = kx 这个函数的图形化表达。对于这个弹簧,我们可以说,它的最大承载力是10,最大变形能力是1,刚度是 10 除以 1 等于 10;不同的弹簧有着不同的承载能力、变形能力和刚度,取决于不同的材料、尺寸等等。比如我换一根更结实的弹簧,这根弹簧的最大承载能力是 14,最大变形能力是 1,刚度为 14 除以 1 等于 14。
不同的弹簧有着不同的承载能力、变形能力和刚度,取决于不同的材料、尺寸等等。比如我换一根更结实的弹簧,这根弹簧的最大承载能力是 14,最大变形能力是 1,刚度为 14 除以 1 等于 14。
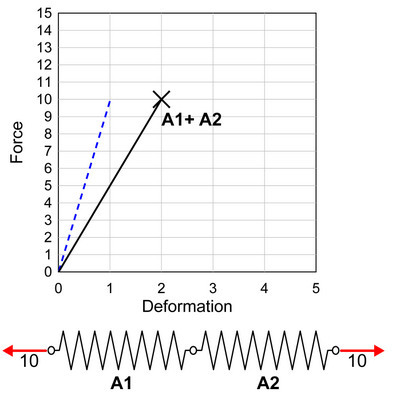
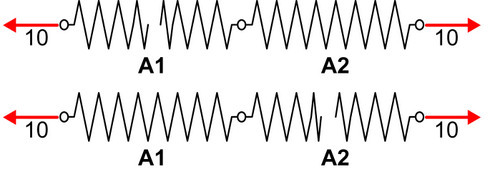
如果我们把两根弹簧连在一起呢?比如说,我们把两根刚度为 10、最大承载力为 10 的弹簧连在一起,组成一根新的弹簧,这根弹簧的性能又如何呢?相信高中物理也讨论过这个问题。这两根连在一起的弹簧,受力相等,总的变形等于两者的变形之和。换言之,这根组合起来的新的弹簧,最大承载力还是 10,最大变形能力变成了 2,而刚度变成了 10 除以 2 等于 5。
如果我们把两根弹簧连在一起呢?比如说,我们把两根刚度为 10、最大承载力为 10 的弹簧连在一起,组成一根新的弹簧,这根弹簧的性能又如何呢?相信高中物理也讨论过这个问题。这两根连在一起的弹簧,受力相等,总的变形等于两者的变形之和。换言之,这根组合起来的新的弹簧,最大承载力还是 10,最大变形能力变成了 2,而刚度变成了 10 除以 2 等于 5。
下面就是有意思的部分了。我们说这根新的弹簧的最大承载力是 10,也就是说,我施加大小为 10的拉力,这根新的弹簧就会断裂。问题来了,我们能确定断裂发生在哪个部位吗?简单说,这根 A1+A2 组成的新弹簧,如果被拉断,断点发生在 A1 那一部分呢还是 A2 那一部分呢?
答案是不知道,或者说是随机的。可能是 A1 被拉断,也可能是 A2 被拉断。注意,我们讨论的是理论问题,所以我们的前提是 A1 和 A2 是完全一样的弹簧。现实世界中没有两片相同的树叶,也没有两根相同的弹簧。但如果我们接受 A1 和 A2 是完全一样的这个假设,那么断裂发生在 A1 还是 A2 就是完全随机的。
答案是不知道,或者说是随机的。可能是 A1 被拉断,也可能是 A2 被拉断。注意,我们讨论的是理论问题,所以我们的前提是 A1 和 A2 是完全一样的弹簧。现实世界中没有两片相同的树叶,也没有两根相同的弹簧。但如果我们接受 A1 和 A2 是完全一样的这个假设,那么断裂发生在 A1 还是 A2 就是完全随机的。
那如果不是两根完全一样的弹簧,而是两根不一样的弹簧呢?比如说,我们把上面这个刚度为10的弹簧和刚度为14的弹簧连在一起。这时候,这根新弹簧 A + B 的最大承载能力是多少呢?是 10 还是 14?答案很显然是 10。因为两根弹簧的受力每时每刻都是相同的,A 最大可以承受 10,B 最大可以承受 14。当外力逐步逐步增大到 10 的时候,A 已经达到极限,啪的一声就断了,而 B 却不会断裂,因为这时候的受力 10 还是小于 B 的最大承载能力 14。换句话说,这其实是个「木桶原理」的实例。木桶能装多少水,取决于组成木桶的木板里最矮的那一个;弹簧组成的串联弹簧的承载力,取决于这些弹簧里承载力最低的那一个
这时候这根新弹簧被拉断,我们能确定断裂发生在哪里吗?理论上说,断裂一定会发生在 A 弹簧上。因为 B 弹簧的承载力大于 A,所以一定是 A 先断。也就是说,通过配置不同的弹簧,断裂的位置不再是随机的,而是可以被控制的。我们想让断裂发生在哪里,就把 A 弹簧放在哪里,将来一旦断裂,断点就肯定会发生在那里。类似的例子就是电路里的保险丝,一旦过载,断点肯定是在保险丝那里,而不是在别的地方,从而保护了电路的其它位置。
这时候这根新弹簧被拉断,我们能确定断裂发生在哪里吗?理论上说,断裂一定会发生在 A 弹簧上。因为 B 弹簧的承载力大于 A,所以一定是 A 先断。也就是说,通过配置不同的弹簧,断裂的位置不再是随机的,而是可以被控制的。我们想让断裂发生在哪里,就把 A 弹簧放在哪里,将来一旦断裂,断点就肯定会发生在那里。类似的例子就是电路里的保险丝,一旦过载,断点肯定是在保险丝那里,而不是在别的地方,从而保护了电路的其它位置。
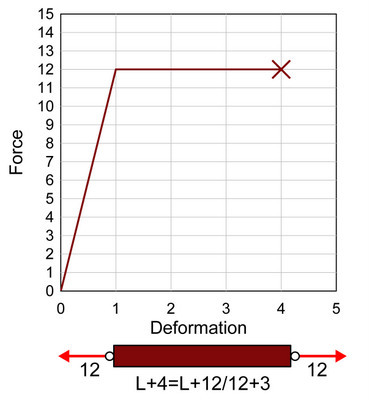
我们也知道,并不是所有的材料都是弹簧,也并不是所有的材料都是拉长到一定程度啪的一声就断了。比如说,大多数金属材料都是延性材料,或者说弹塑性材料,也就是说,这些材料不仅仅像弹簧那样会发生弹性变形,还会发生后面的塑性变形。比如这样一根钢棒,逐渐逐渐加大外力,一开始,它表现的其实就是一根弹簧,变形随着外力成比例的线性增加,刚度为 12。当外力加大到 12,变形变成 1 的时候,这根钢棒开始进入塑性阶段。什么意思呢?意思就是变形持续增加,但是外力不再增加。受力变形图从一条斜率为 k 的斜线变成平行于 x 轴的水平线。
举个简单的例子,一根钢尺子,如果你轻轻的掰它,一松手尺子自己就会弹回原来的形状。为什么呢?因为你施加的外力还不够大,尺子还处在斜率为 k 的斜线阶段,也就是所谓的弹性阶段。如果你狠狠心,下狠手掰尺子,钢尺子会断成两截吗?一般不会。通常来说,钢尺子会被你掰弯成 U 形,松手之后也不会再弹回去。这又是为什么呢?因为你施加的外力足够大,钢尺子进入了水平线阶段,也就是所谓的塑性阶段。这时候承载力已经不能再增加,但是位移可以持续增加,所以尺子就被掰成了 U 形。
当然,尺子变成 U 形之后,如果你继续用力掰,总归可以把尺子掰断。也就是说,材料在进入塑性阶段之后,还是会有最终的破坏点。比如我们的这个例子里,这根钢棒在位移为 1 的时候进入塑性,然后一直到位移为 4 的时候断裂。我们把这两者的比值,也就是 4 除以 1 等于 4,看作这根钢棒的延性比。换句话说,延性比越大,延性越好,在最终破坏之前的变形越大。
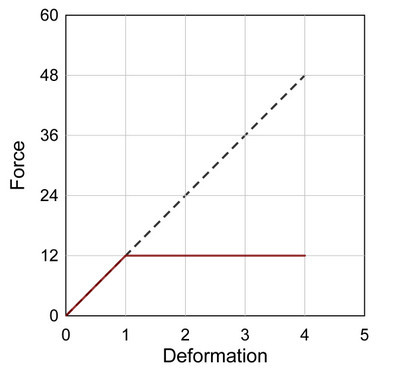
为什么我们需要弹塑性材料呢?为什么不能全用弹簧呢?我们可以比较一下我们例子里的这个弹塑性材料和完全弹性材料的区别。如果这根钢棒变成一根刚度相同的弹簧,那么达到同样的变形,弹簧的受力要远远高于钢棒。换言之,弹簧必须非常非常结实,结实到足够承受大小为 48 的外力,才能做到变形为 4。而对于弹塑性的钢棒来说,不需要那么结实就可以,只需要承受大小为 12 的外力,此后就进入塑性阶段了。也就是说,我们想要的是比较大的变形能力,同时,与最大的变形相对应的受力可以尽可能的小一些。而这正是弹塑性材料的特征,也是为什么我们要在抗震里应用弹塑性材料的原因。
如果这根钢棒变成一根刚度相同的弹簧,那么达到同样的变形,弹簧的受力要远远高于钢棒。换言之,弹簧必须非常非常结实,结实到足够承受大小为 48 的外力,才能做到变形为 4。而对于弹塑性的钢棒来说,不需要那么结实就可以,只需要承受大小为 12 的外力,此后就进入塑性阶段了。也就是说,我们想要的是比较大的变形能力,同时,与最大的变形相对应的受力可以尽可能的小一些。而这正是弹塑性材料的特征,也是为什么我们要在抗震里应用弹塑性材料的原因。
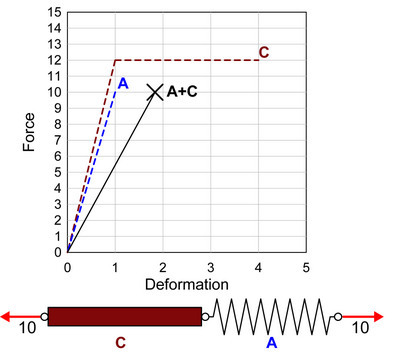
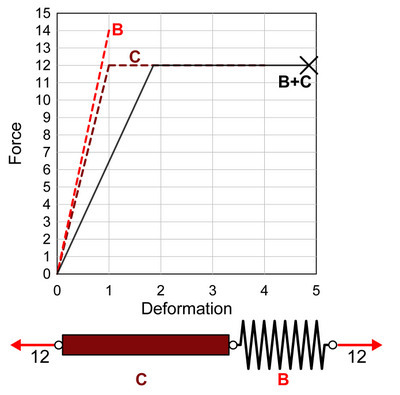
接下来呢,我们就把这根弹塑性的钢棒 C 和弹簧 A 连接在一起钢棒 C 的承载力是 12,弹簧 A 的承载力是10,它俩连在一起,根据木桶原理,最大承载力是 10。当外力为 10 的时候,弹簧 A 被拉断,此时的变形为弹簧 A 的 1 再加上钢棒 C 的10/12,只有 1.83。简单说,钢棒 C 根本没有发挥什么作用。还没等它的塑性阶段大显神威呢,它的猪队友——弹簧 A——已经先挂了。
钢棒 C 的承载力是 12,弹簧 A 的承载力是10,它俩连在一起,根据木桶原理,最大承载力是 10。当外力为 10 的时候,弹簧 A 被拉断,此时的变形为弹簧 A 的 1 再加上钢棒 C 的10/12,只有 1.83。简单说,钢棒 C 根本没有发挥什么作用。还没等它的塑性阶段大显神威呢,它的猪队友——弹簧 A——已经先挂了。结论就是,如果钢棒强于弹簧,则这个组合很糟糕,弹簧变成了猪队友,钢棒被猪队友拖累,还没发展到大后期呢就跟着猪队友一起被团灭了。
那如果我们把钢棒 C 跟弹簧 B 连在一起呢,这时候,弹簧 B 就不是猪队友了,因为它的承载力要大于钢棒 C,所以当外力增大到 12 的时候,钢棒 C 进入屈服,变形开始持续增大,而弹簧 B 可以轻松的承载大小为 12 的外力而不破坏。整个系统的变形可以一直持续增大,直到最大变形等于弹簧 B 的变形 12/14 再加上钢棒 C 的变形 4 等于 4.86。所以呢,
这时候,弹簧 B 就不是猪队友了,因为它的承载力要大于钢棒 C,所以当外力增大到 12 的时候,钢棒 C 进入屈服,变形开始持续增大,而弹簧 B 可以轻松的承载大小为 12 的外力而不破坏。整个系统的变形可以一直持续增大,直到最大变形等于弹簧 B 的变形 12/14 再加上钢棒 C 的变形 4 等于 4.86。所以呢,如果弹簧强于钢棒,则这个组合就很理想,钢棒的变形能力得到了最大发挥,而弹簧可以有效的传递外力,不会过早破坏,圆满的完成了「扶上马送一程」的任务,然后笑看高等级的大后期英雄——钢棒——发挥最大的变形能力。
最终的结论,想要变形能力,同一个系统里的弹塑性构件的承载力就必须小于弹性构件的承载力,或者说,系统里的弹性部分的承载力必须大于贡献了绝大部分变形的弹塑性部分的承载力。
简单说,弹簧的承载力要大于钢棒,强弹簧弱钢棒。类比造句,强柱弱梁,强剪弱弯,强节点弱杆件……
这里的「强」和「弱」,并不是绝对意义上的强弱,也不是破坏的先后顺序。并不是说梁用 C30 的混凝土,柱子就必须得用 C50 的;也不是说破坏的时候一定是梁先断,柱子还屹立不倒;更不是说既然「强柱弱梁」可以,那「强柱强梁」岂不是更好?
「强柱弱梁」,相当于我们的弹簧 B 加钢棒 C,变形能力很好,这正是我们想要的;「弱柱强梁」,相当于我们的弹簧 A 加钢棒 C,变形能力不好,塑性变形能力完全没有发挥,既浪费了钢棒的能力,效果又很差;「强柱强梁」,相当于我们这里的两个弹簧连在一起,变形能力一般,多用了很多材料,而且你还永远不知道断裂究竟会发生在哪个弹簧上面。