柔性吊桥是指不设加劲梁或加劲梁高度很小的吊桥,因其桥面系构造简单、耗钢量小、桥面架设和维护方便、桥型美观、造价低等特点,适用于我国地形地势复杂的西南山区。柔性悬索桥中大部分荷载由缆索承担,虽在设计时考虑了一定的安全系数,但随着时间的推移,车辆荷载作用下桥面将随悬索形状的改变而产生 S 形的变形,不利于行车安全,同时,因超载、疲劳等不确定因素会导致吊杆破损,给吊桥的安全运营带来威胁,加上山区自然环境恶劣,柔性吊桥疲劳寿命问题日益显现。近年来,我国因吊杆断裂导致桥梁垮塌的事件频频发生。因此需要对柔性吊桥吊杆进行优化设计,以保障桥梁的安全高效。
以车里格桥为例,研究吊杆的破损安全优化设计方案,借助有限元软件计算原桥吊杆与基于应力差优化吊杆的内力,对比分析其是否能够实现寿命差。主要内容包括:1) 通过理论分析和计算分析提出由内外部分组成的单吊杆优化方案代替传统的平行双吊杆,并对其应力差及强度差的“破损安全吊杆系统”进行评估。2) 介绍一种通过改变应力幅达到破损安全的设计方法,并与普通单吊杆进行计算对比。3) 用全动力模拟方法来模拟吊杆的骤断情况探究弹性块刚度对寿命差破损安全吊杆的破断影响。4) 通过改变吊杆内外部分的面积比及弹性块的刚度探究了寿命差破损安全吊杆的优化效果。
结果表明吊杆的破损安全优化设计方案并不能实现明显的寿命差,在上述基础上提出在安全束下方添加橡胶垫块的方案,通过调整应力幅差达到破损安全优化设计的目的,并通过静、动力分析验证其优化效果;最后通过调整截面参数和橡胶垫块刚度来探究破损安全吊杆的受力特点,结果表明:截面参数的调整对吊杆受力影响不大,橡胶垫刚度的改变对吊杆应力幅的影响较为明显。
西南地区山峦重叠、沟壑纵横,多为高山峡谷地带,交通设施的建设成本远高于平原地带,因此自重轻、造价低、跨度大、施工简便且周期短的柔性吊桥在山区桥梁中所占比重较大。作为一种刚度较小的柔性结构,服役中其大部分的荷载均由缆索系统承担,虽然设计时考虑了一定的安全系数,但随着时间的推移,因大幅超载、疲劳等不确定因素会导致吊杆破损,给吊桥的安全运营带来威胁。
吊杆断裂的原因大致可以分为两种:一是塑性破坏,指吊杆受到远大于破断力的荷载,达到承载能力极限状态后破坏;二是疲劳破坏,钢结构总会存在微观裂纹或类似的缺陷,车辆荷载的反复作用加上外界环境的不断锈蚀会导致裂纹逐渐扩展,直至到达临界状态后在一个远小于设计的荷载作用下发生断裂。近年来,有学者提出了忽略吊杆破断原因, 只 关注剩余结构强度的破损安全设计理念。因此,人们开始研究以破损安全理论为基础的吊杆优化系统,来提高桥梁整体结构的安全性。目前较为常用的有基于应力差和强度差的破损安全吊杆系统。以车里格桥为对象,借助有限元软件计算原桥吊杆和基于应力差优化吊杆的内力,对比分析吊杆的破损安全优化设计方案是否能够实现寿命差(两根或多根吊杆先后破坏的时间差)。并在此基础上提出在安全束下方添加橡胶垫块的方案,并验证其可行性及优化效率。
1 吊杆优化方案分析
1.1 吊杆构造
Suzumura 等的研究发现:钢丝的临界湿度为60%左右,一旦超过界限,吊杆的腐蚀将急剧增加,相对湿度越大则腐蚀速率越明显;汤国栋等对钢索失效及断裂等问题研究得出:在外界环境和荷载的共同作用下,吊杆的外圈钢丝会更快出现腐蚀现象。而车里格桥为跨金沙江而设,空气湿度较大,吊杆在运营过程中易发生湿腐蚀,因此本文优化所用吊杆,并在双吊杆优化方案的基础上做出了结构形式上的变更,使用内外吊杆形式代替传统的平行双吊杆,单吊杆体系横截面示意如图 1 所示。
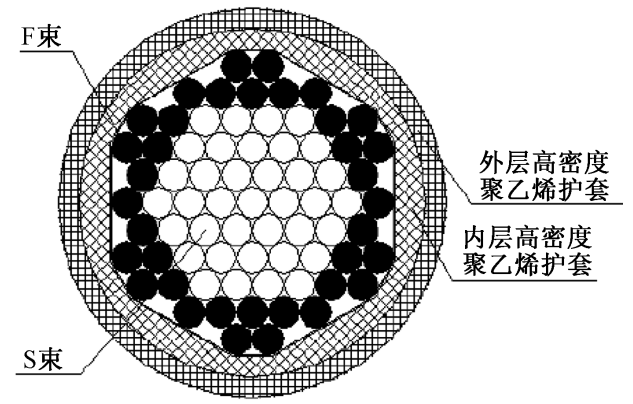
以破损安全理论为基础构建的破损安全优化吊杆应具备以下功能:
1) F 束和 S 束分开锚固,并且能够单独承载,F束断裂时,S 束能承受住瞬间增大的内力,不会造成“多米诺” 式的连环断裂,且提供足够的时间更换吊杆。
2) 优化方案的材料用量不大于原桥吊杆,即无论是新桥建设或是旧桥加固,都能够完全取代普通吊杆。
1.2 计算分析
目前,大部分吊杆的寿命预测都是使用应力-寿命曲线(S-N 曲线)来实现的,其基本表达式为幂函数,即:
ΔSmN = C (1)
式中: m 和 C 为通过疲劳加载试验得到的与材料性质、试样形式、应力比和加载方式等相关的参数。ΔS 为外加应力幅;N 为在 ΔS 的应力幅作用下构件发生破坏的应力循环次数,且这种破坏往往属于脆性破坏。
从式(1)可以看出,构件的疲劳寿命仅与构件的材料常数、外加应力幅大小以及应力幅循环次数有关,疲劳损伤累计理论同样认为,影响疲劳断裂的主要参量为应力幅和循环频率。
1.2.1 基于应力差的破损安全优化吊杆
令 S 束和 F 束的材料强度相同,S 束的截面面积大于 F 束( S、F 束面积之和等于原吊杆),对 F 束进行超张拉,使应力 σF( F 束应力) > σS ( S 束应力)。
车里格桥原有吊杆方案为 1ϕ36(6×7+IWS 钢丝股芯) 镀锌钢芯钢绳,钢绳强度为 1770 MPa,单根破断拉力为 824 kN。为方便计算,将吊杆替换为25 根标准强度不变的 ϕs7 高强钢丝。由于本小节只探究通过改变应力差来实现破损安全吊杆的设计,将 F 束和 S 束的面积比定为 2∶3 来进行计算。F 束采用壁厚为 4 mm 的桶状钢丝束,S 束采用直径为 28 mm 的圆形钢丝束。
分别建立单吊杆和破损安全吊杆模型,赋予两个模型相同的初始内力,保证在成桥状态下,两个模型的吊杆内力基本一致,并计算得到两个模型在成桥状态的位移基本相同,即验证两个模型的成桥状态基本一致。之后分别进行倒拆分析,获得单吊杆模型和破损安全吊杆模型的空缆状态。以两个空缆线形及主缆的无应力长度分别建立两个正装模型。以索单元无应力长度为自变量,通过反复调试使 F束在恒载下比 S 束多 10 kN 的力,然后加入活载进行分析,本次模型车辆荷载选用刘海证制定的山区低等级公路疲劳荷载谱中损伤贡献率最大的第三类车荷载。
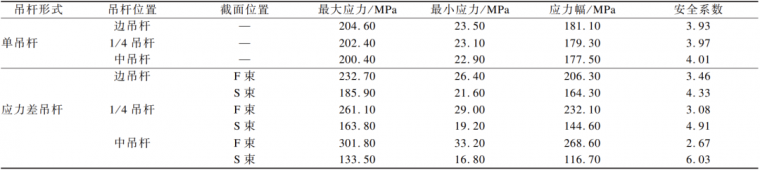
由于吊桥吊杆众多,因篇幅所限,仅选取具有代表性的中吊杆、边吊杆以及 1/4 处吊杆进行研究。具体受力情况如表 1 所示。
表 1 应力差吊杆受力情况
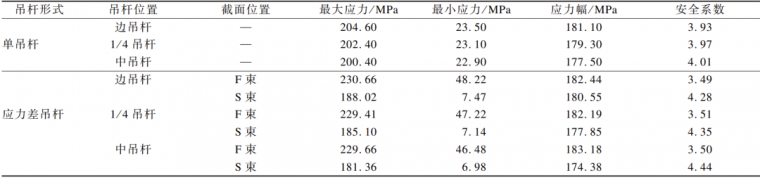
可见:将单吊杆替换成应力差吊杆后,通过对 F束超张拉使内力重分配,吊杆的应力有了明显变化,均较单吊杆的应力上浮了 20~30 MPa,但应力幅却变化不大,依然与单吊杆相差无几。通过 S-N 曲线的基本表达式可以判断:超张拉无法有效控制内外吊杆的先后破断。
1.2.2 基于强度差的破损安全优化
当 F、S 束的应力和应力幅均相同时,如果改变S 束的制作材质,使两种吊杆具有相异的材料常数,例如使 F 束的疲劳强度小于 S 束的疲劳强度,那么在疲劳和锈蚀的耦合作用下也能实现先后破断,达到破损安全设计的目的。这种方法难以在施工过程中实现,但随着吊杆越来越倾向于成品索,这种破损安全吊杆的设计方式可以作为一种全新的吊杆产品进行研发
强度差吊杆设计方法是一种较好的新型吊杆设计理念,但具体实操情况有待后续研发;应力差破损安全吊杆设计方法能改变吊杆的应力,但对应力幅的改变微乎其微,且 S、 F 两束是锚固在一起的,有的工程技术无法对其进行超张拉使内外束产生应力差。因此本文以不等应力幅带来的寿命差为思路,介绍一种破损安全优化吊杆设计方法。
2 寿命差吊杆优化方案分析
2.1 吊杆构造
与 1.2.1 节提出的破损安全吊杆设计方案相比,本节优化方案依然使用内外吊杆构造的截面形式,在此基础上于 S 束与横梁锚固点处添加了一块橡胶垫块,具体布置如图 2 所示。
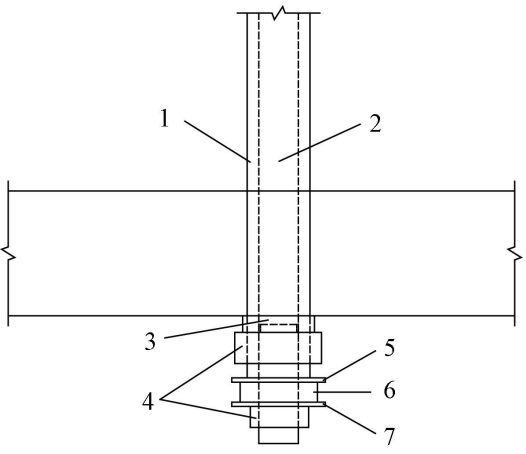
1—主承重束,即 F 束;2—安全束,即 S 束;3—钢垫板;4—螺栓;5—橡胶垫块上垫块;6—橡胶垫块;7—橡胶垫块下垫块。
图 2 橡胶垫块布置
设 F 束面积为 AF ,S 束面积为 AS ,假设 F、S 束的弹性模量为 E,刚度分别为 KF 和 KS ,橡胶垫块的刚度为 KP ,吊杆整体受力为 F ,可推导出 S 束的整体刚度为:
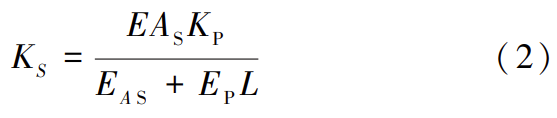
式中:L 为吊杆长度。
根据同一吊点刚度分配原则,可计算出 F 束和S 束的内力分别为:
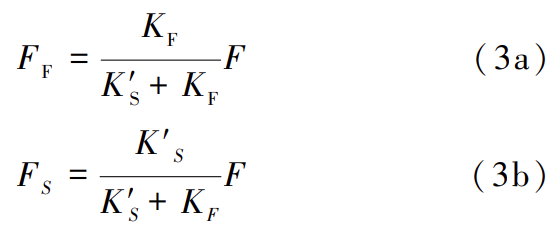
2.2 计算分析
采用有限元软件建立车里格桥模型并在吊杆与横梁锚固点处加橡胶垫块,用弹性连接来模拟橡胶垫块。拟定 AF/AS= 2/3,橡胶垫块厚度为 100 mm,刚度为 30000 kN/m,模型中设置弹性连接在 Dy 、Dz 方向固接, Dx 方向刚度为 30000 kN/m。其具体受力情况如表 2 所示。
从表 2 可以看出,在 S 束下方设置橡胶垫块后,吊杆受力较之前有了显著改变,三组吊杆的应力幅均有了较大程度的增加:边吊杆最小,为 42 MPa,其次是1/4 处吊杆,中吊杆最大,为 151.9 MPa。由此得出结论:在 S 束下方添加弹性块可以明显改变两束的应力及应力幅,从而改变其寿命差,达到先后破断的目的。
表 2 寿命差吊杆受力情况
3 寿命差吊杆受力分析
3.1 动力响应分析
通过第 2 节对两种破损安全吊杆的静力受载情况进行对比,证实了寿命差破损安全吊杆设计方案可以有效改变两束吊杆的寿命差。本小节将通过改变弹性块的刚度来探究寿命差破损安全吊杆的 F束断裂时,S 束的动力响应。
采用全动力模拟方法来模拟 F 束的骤断情况,荷载的上升时长取两个结构基本周期;构件的失效时长取 1/20 结构基本周期;分析方法使用直接积分法,积分时间步长选取关注结果中总贡献率超过80%的所有振型中频率最高的振型所对应的周期的1/20;结构分析采用 Rayleigh 阻尼 ,即:
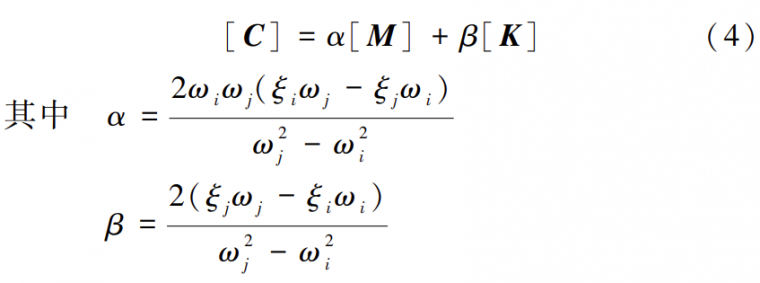
式中: α 和 β 分别为质量阻尼系数和刚度阻尼系数;ωi 和 ωj 分别为结构的第 i、j 阶固有频率;ξi 和 ξj则分别是与固有频率相对应的阻尼比。考虑到全桥均为钢结构,阻尼系数采用 0.02。
本次计算所用吊杆面积比沿用静力分析时所用面积比,即 AF/AS= 2/3, 弹性块刚度分别选取 10,100,1000,10000,100000 kN/m 进行全动力模拟,F 束骤断时 S 束动力响应结果见图 3。
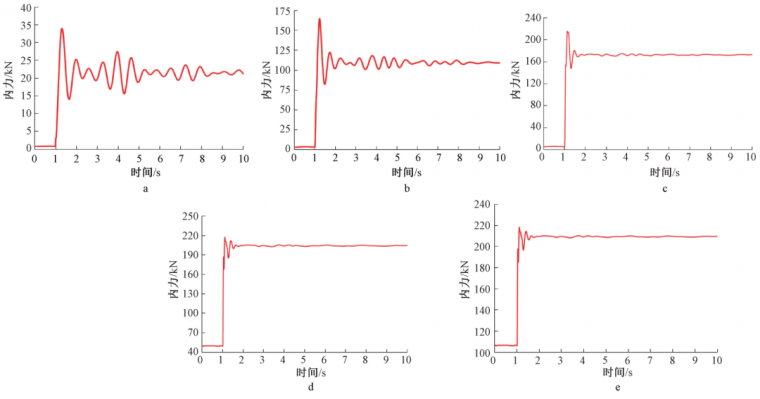
a—刚度 10 kN/m; b—刚度 100 kN/m; c—刚度 1000 kN/m; d—刚度 10000 kN/m; e—刚度 100000 kN/m。
图 3 S 束动力响应结果
为了更直观地对比不同刚度下 S 束的动力响应,将上述图形整理成如表 3 所示。可以看出,与S0 的比值以及动力放大系数( Smax/Ss ) 随弹性块刚度增大而减小。
表 3 动力响应结果
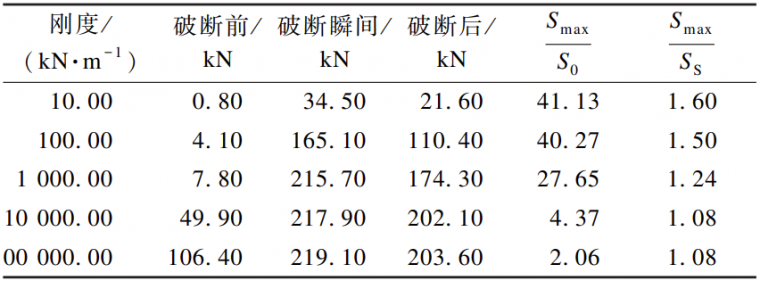
注:S0、Smax、SS 分别指 S 束的初内力、F 束破断瞬间 S 束的最大内力以及最终内力
3.2 寿命差吊杆优化性能分
在不增加材料用量的情况下,调整内外吊杆的面积比,拟定以下 5 个面积比方案。方案1: AF/AS=8/17;方案2: AF/AS= 9/16;方案3: AF/AS= 10/15;方案4: AF/AS= 11/14;方案5: AF/AS= 12/13。将 5 个方案分别采用刚度为 10000, 20000, 30000,40000,50000 kN/m 的弹性块进行计算分析,计算结果除考虑吊杆破断前静力受载情况外,还将考虑吊杆破断瞬间动力响应情况及吊杆破断后由 S 束单独承载时的静力受载情况。由于篇幅有限,仅列出中吊杆的应力计算结果,如表 4 所示。
表 4 中吊杆应力计算结果
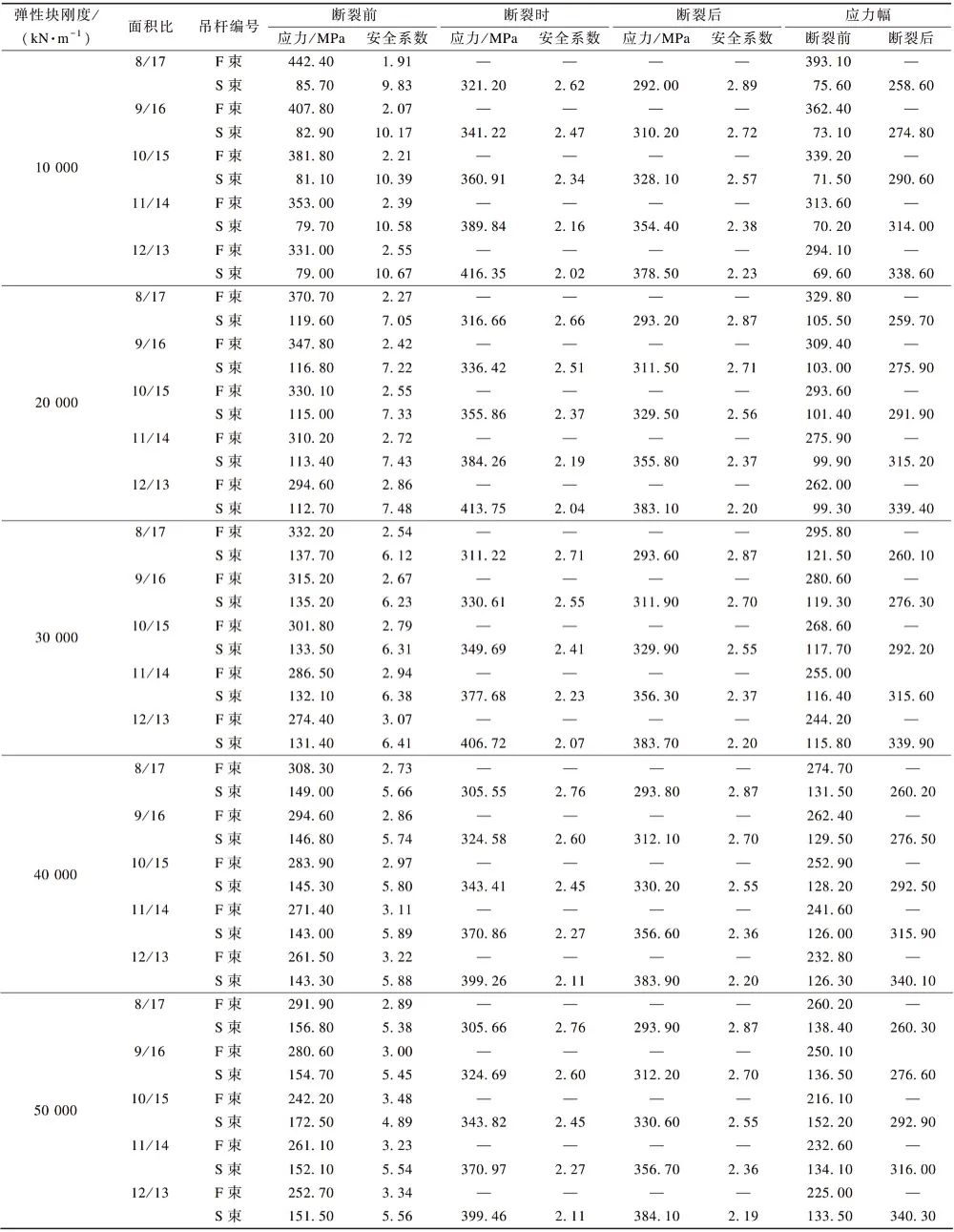
从表 4 可以看出,正常运营阶段相同弹性块作用下,S、F 束的面积比变化对吊杆安全系数不会产生较大的影响;但随着弹性块刚度的增大,F 束的安全系数在增大,S 束的安全系数在减小,当弹性块刚度为 10000 kN/m 时,F 束的安全系数不满足要求。为了更好地确定最佳的面积比和弹性块刚度来达到最优方案的目的,在面积比方案 1~4,弹性块刚度20000~50000 kN/m 情况下,讨论构件的应力循环次数来确定吊杆最优方案。
由于缺乏吊杆材料的疲劳试验数据,因此本文将采用美国得克萨斯州立大学 Paulson 等在对不同厂家生产的 700 余根钢绞线的疲劳试验结果的统计分析和补充试验的基础上所提出的 S-N 曲线,即:
lg N = 13.93 - 3.5lg Δσ (5)
本次计算所用吊杆无需考虑多车效应及横向车效应,因此认为 F 束破断前 S 束的应力幅将经历与F 束应力幅相同的应力循环次数,根据 Miner 准则(线性疲劳累积损伤理论) ,S 束疲劳破断应满足下列条件:
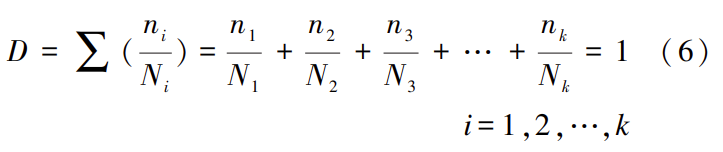
式中:ni 为应力幅经历的第 i 次循环次数;Ni 为构件容许应力经历的第 i 次总循环次数。
联合式(5)和式(6),计算得出 F 束断裂后 S 束容许应力循环次数及次数比见表 8、表 9。
表 8 应力容许循环次数
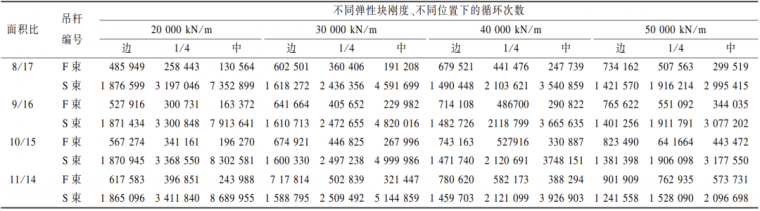
表 9 应力容许循环次数比

在材料用量不变的情况下,当循环次数比过大时,在正常运营阶段 F 束较容易退出工作;当循环次数比过小时,说明两束寿命差不大,这违背了破损安全吊杆的设计初衷。综合考虑,应力循环次数比在 2~4 之间为最佳。综上所述:边吊杆最优方案的刚度为 20000~40000 kN/m,面积比为方案 1~4;1/4 跨吊杆最优方案的刚度为 40000~50000 kN/m,面积比为方案 2~4; 中吊杆最优方案的刚度为50000 kN/m,面积比为方案 4。
4 结 论
1)利用内外部分组成的单吊杆优化方案代替传统的平行双吊杆,对应力差及强度差的“破损安全吊杆系统” 进行评估,并结合 S-N 曲线分析两种方案的优化效果。计算结果表明:应力差吊杆在一定程度上改变了吊杆应力,但并未改变应力幅,对两束吊杆的寿命影响甚微,在不考虑钢丝锈蚀的情况下,不具有足够的安全储备;强度差吊杆在理论上可以达到破损安全的目的,但很难通过目前的施工技术实现,可作为一种新型成品吊杆来研发。
2) 介绍了一种通过改变应力幅达到破损安全的设计方法,并与普通单吊杆进行计算对比,结果表明:在 S 束下方添加弹性块可以有效改变两束吊杆的应力差和应力幅差,达到先后破断的目的。
3) 以全动力模拟方法进行了吊杆的断裂模拟,通过改变弹性块刚度探究了寿命差破损安全吊杆的F 束破断对 S 束的影响。结果表明:如果 S 束下方添加的弹性块刚度不同,动力放大系数也会有所差别,随着刚度逐渐增大,动力响应越接近静力分析结果。
4) 通过改变 F、S 束的面积比及弹性块的刚度探究了寿命差破损安全吊杆的优化效果,结果表明:弹性块刚度的改变对吊杆的应力幅影响较为明显,而面积比的改变对应力幅影响不大;利用吊杆安全系数和应力循环次数比作为优化效果评价标准,得出: 边吊杆最优方案的刚度为 20000~40000 kN/m,面积比为方案 1~4;1/4 跨吊杆最优方案的刚度为 40000~50000 kN/m,面积比为方案2~4;中吊杆最优方案的刚度为 50000 kN/m,面积比为方案 4。
